
Question Number 200741 by Rydel last updated on 22/Nov/23
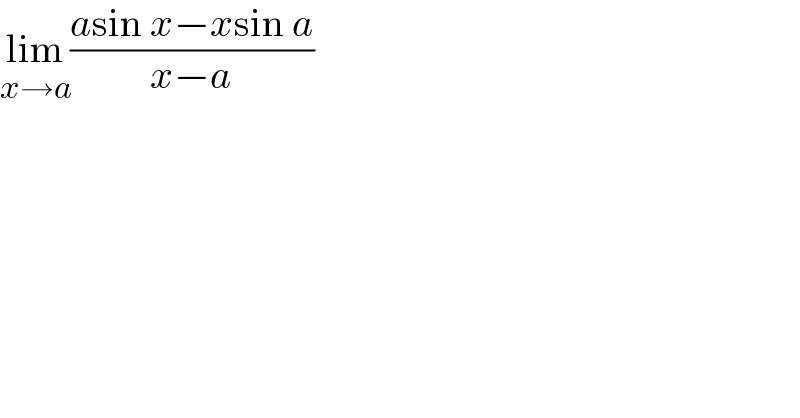
$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{a}\mathrm{sin}\:{x}−{x}\mathrm{sin}\:{a}}{{x}−{a}} \\ $$
Commented by JDamian last updated on 22/Nov/23
really?
Answered by JDamian last updated on 22/Nov/23
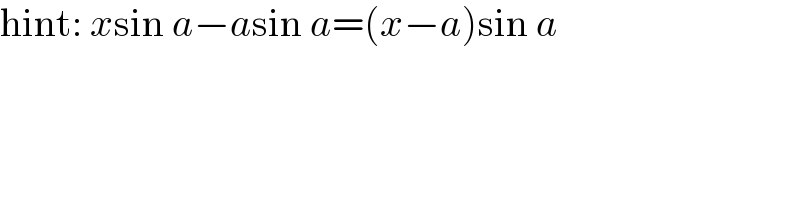
$$\mathrm{hint}:\:{x}\mathrm{sin}\:{a}−{a}\mathrm{sin}\:{a}=\left({x}−{a}\right)\mathrm{sin}\:{a} \\ $$
Commented by Rydel last updated on 22/Nov/23
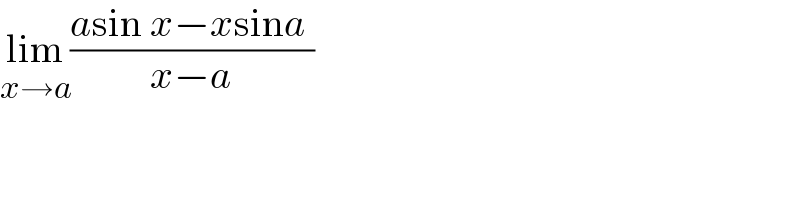
$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{a}\mathrm{sin}\:{x}−{x}\mathrm{sin}{a}\:}{{x}−{a}} \\ $$
Answered by MM42 last updated on 22/Nov/23
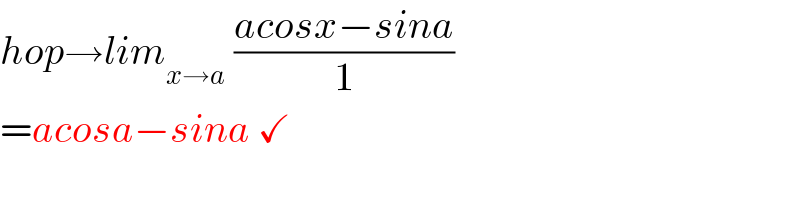
$${hop}\rightarrow{lim}_{{x}\rightarrow{a}} \:\frac{{acosx}−{sina}}{\mathrm{1}} \\ $$$$={acosa}−{sina}\:\checkmark \\ $$
Answered by tri26112004 last updated on 23/Nov/23
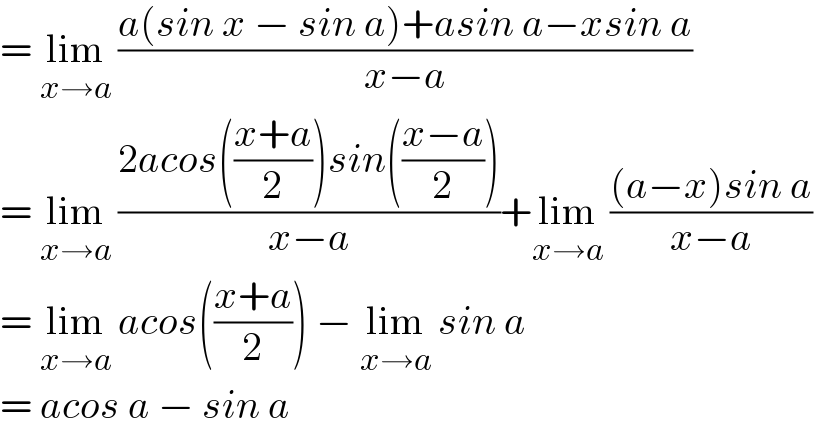
$$=\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{a}\left({sin}\:{x}\:−\:{sin}\:{a}\right)+{asin}\:{a}−{xsin}\:{a}}{{x}−{a}} \\ $$$$=\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{\mathrm{2}{acos}\left(\frac{{x}+{a}}{\mathrm{2}}\right){sin}\left(\frac{{x}−{a}}{\mathrm{2}}\right)}{{x}−{a}}+\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{\left({a}−{x}\right){sin}\:{a}}{{x}−{a}} \\ $$$$=\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:{acos}\left(\frac{{x}+{a}}{\mathrm{2}}\right)\:−\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:{sin}\:{a} \\ $$$$=\:{acos}\:{a}\:−\:{sin}\:{a} \\ $$
Commented by Rydel last updated on 23/Nov/23
$${thank}\:{you}\:{very}\:{much} \\ $$
Answered by MM42 last updated on 23/Nov/23

$${x}−{a}={u} \\ $$$$\Rightarrow{lim}_{{u}\rightarrow\mathrm{0}} \:\frac{{asin}\left({u}+{a}\right)−\left({u}+{a}\right){sina}}{{u}} \\ $$$$={lim}_{{u}\rightarrow\mathrm{0}} \:\frac{{asinucosa}+{asinacosu}−{usina}−{asina}}{{u}} \\ $$$$={lim}_{{u}\rightarrow\mathrm{0}} \left(\:\frac{{sinu}}{{u}}{acosa}−{sina}−\frac{\mathrm{1}−{cosu}}{{u}}{asina}\right) \\ $$$$={acosa}−{sina} \\ $$$$ \\ $$
