
Question Number 168821 by mathlove last updated on 18/Apr/22
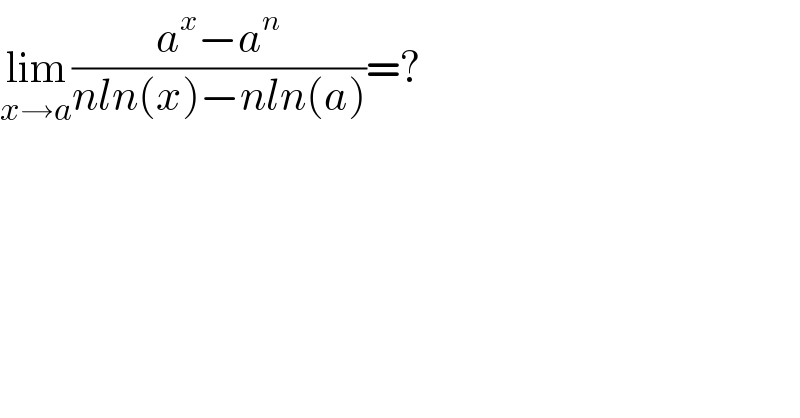
$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{a}^{{x}} −{a}^{{n}} }{{nln}\left({x}\right)−{nln}\left({a}\right)}=? \\ $$
Answered by alephzero last updated on 18/Apr/22
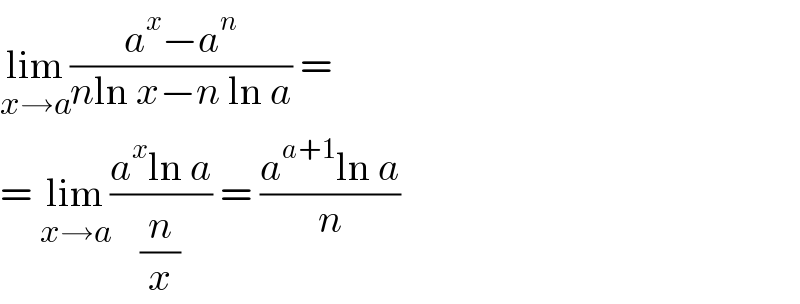
$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{a}^{{x}} −{a}^{{n}} }{{n}\mathrm{ln}\:{x}−{n}\:\mathrm{ln}\:{a}}\:= \\ $$$$=\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{a}^{{x}} \mathrm{ln}\:{a}}{\frac{{n}}{{x}}}\:=\:\frac{{a}^{{a}+\mathrm{1}} \mathrm{ln}\:{a}}{{n}} \\ $$
Commented by aleks041103 last updated on 18/Apr/22
![You′re using l′hopital′s rule, but to do so the limit must be of the form [(0/0)] or [(∞/∞)]. For this limit the denominator does go to 0, but the numerator goes to 0 only if n=a. If a=n, then your answer is correct, otherwise the limit goes to ±∞ depending on which is bigger a^a or a^n .](Q168836.png)
$${You}'{re}\:{using}\:{l}'{hopital}'{s}\:{rule},\:{but}\:{to}\:{do}\:{so} \\ $$$${the}\:{limit}\:{must}\:{be}\:{of}\:{the}\:{form}\:\left[\frac{\mathrm{0}}{\mathrm{0}}\right]\:{or}\:\left[\frac{\infty}{\infty}\right]. \\ $$$${For}\:{this}\:{limit}\:{the}\:{denominator}\:{does}\:{go}\:{to}\:\mathrm{0}, \\ $$$${but}\:{the}\:{numerator}\:{goes}\:{to}\:\mathrm{0}\:{only}\:{if}\:{n}={a}. \\ $$$${If}\:{a}={n},\:{then}\:{your}\:{answer}\:{is}\:{correct}, \\ $$$${otherwise}\:{the}\:{limit}\:{goes}\:{to}\:\pm\infty\:{depending} \\ $$$${on}\:{which}\:{is}\:{bigger}\:{a}^{{a}} \:{or}\:{a}^{{n}} . \\ $$
Commented by alephzero last updated on 19/Apr/22
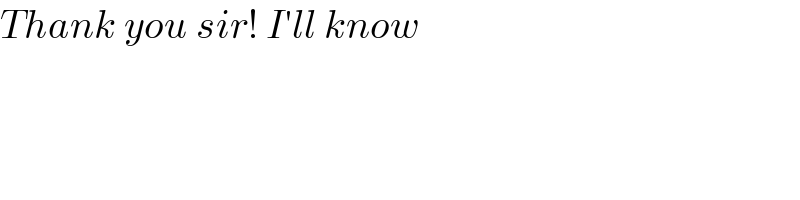
$${Thank}\:{you}\:{sir}!\:{I}'{ll}\:{know} \\ $$
