Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 169479 by cortano1 last updated on 01/May/22

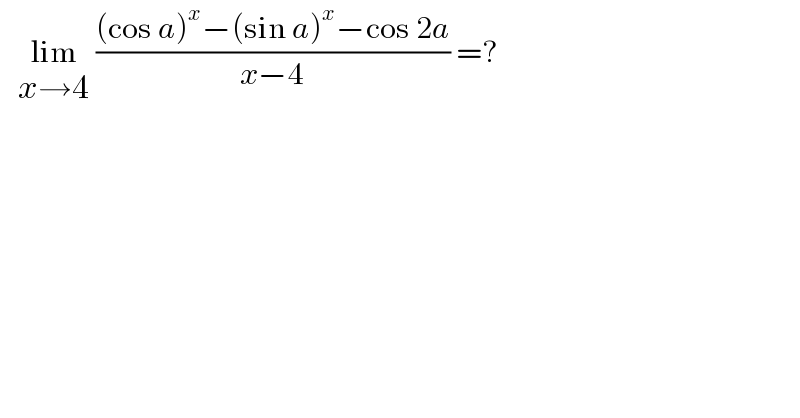
lim_(x→4) (((cos a)^x −(sin a)^x −cos 2a)/(x−4)) =?

$$\:\:\:\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\:\frac{\left(\mathrm{cos}\:{a}\right)^{{x}} −\left(\mathrm{sin}\:{a}\right)^{{x}} −\mathrm{cos}\:\mathrm{2}{a}}{{x}−\mathrm{4}}\:=? \\ $$

Commented by infinityaction last updated on 01/May/22

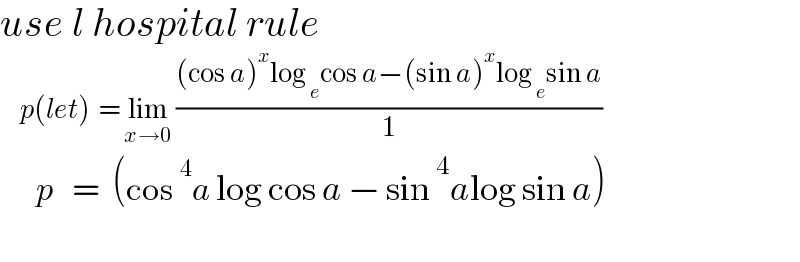
use l hospital rule p(let) = lim_(x→0) (((cos a)^x log _e cos a−(sin a)^x log _e sin a)/1) p = (cos^4 a log cos a − sin^4 alog sin a)

$${use}\:{l}\:{hospital}\:{rule} \\ $$$$\:\:\:\:\:{p}\left({let}\right)\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{cos}\:{a}\right)^{{x}} \mathrm{log}\:_{{e}} \mathrm{cos}\:{a}−\left(\mathrm{sin}\:{a}\right)^{{x}} \mathrm{log}\:_{{e}} \mathrm{sin}\:{a}}{\mathrm{1}} \\ $$$$\:\:\:\:\:\:{p}\:\:\:=\:\:\left(\mathrm{cos}\:^{\mathrm{4}} {a}\:\mathrm{log}\:\mathrm{cos}\:{a}\:−\:\mathrm{sin}\:^{\mathrm{4}} {a}\mathrm{log}\:\mathrm{sin}\:{a}\right) \\ $$$$\:\:\:\: \\ $$

Commented by cortano1 last updated on 01/May/22

not correct

$${not}\:{correct} \\ $$

Answered by greougoury555 last updated on 01/May/22

let h(x)= (cos α)^x −(sin x)^x h(4)= (cos α)^4 −(sin α)^4 = cos 2α L= lim_(x→4) (((cos α)^x −(sin α)^x −cos 2α)/(x−4)) L= lim_(x→4) ((h(x)−h(4))/(x−4)) = h ′(4) h′(x)= (d/dx) [ (cos α)^x −(sin α)^x ] h′(x) = (cos α)^x ln (cos α)−(sin α)^x ln (sin α) L= h′(4)=(cos α)^4 ln (cos α) −(sin α)^4 ln (sin α)

$$\:{let}\:{h}\left({x}\right)=\:\left(\mathrm{cos}\:\alpha\right)^{{x}} −\left(\mathrm{sin}\:{x}\right)^{{x}} \\ $$$$\:{h}\left(\mathrm{4}\right)=\:\left(\mathrm{cos}\:\alpha\right)^{\mathrm{4}} −\left(\mathrm{sin}\:\alpha\right)^{\mathrm{4}} =\:\mathrm{cos}\:\mathrm{2}\alpha \\ $$$$\:{L}=\:\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\:\frac{\left(\mathrm{cos}\:\alpha\right)^{{x}} −\left(\mathrm{sin}\:\alpha\right)^{{x}} −\mathrm{cos}\:\mathrm{2}\alpha}{{x}−\mathrm{4}} \\ $$$$\:{L}=\:\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\:\frac{{h}\left({x}\right)−{h}\left(\mathrm{4}\right)}{{x}−\mathrm{4}}\:=\:{h}\:'\left(\mathrm{4}\right) \\ $$$$\:{h}'\left({x}\right)=\:\frac{{d}}{{dx}}\:\left[\:\left(\mathrm{cos}\:\alpha\right)^{{x}} −\left(\mathrm{sin}\:\alpha\right)^{{x}} \:\right] \\ $$$$\:{h}'\left({x}\right)\:=\:\left(\mathrm{cos}\:\alpha\right)^{{x}} \:\mathrm{ln}\:\left(\mathrm{cos}\:\alpha\right)−\left(\mathrm{sin}\:\alpha\right)^{{x}} \:\mathrm{ln}\:\left(\mathrm{sin}\:\alpha\right) \\ $$$$\:{L}=\:{h}'\left(\mathrm{4}\right)=\left(\mathrm{cos}\:\alpha\right)^{\mathrm{4}} \:\mathrm{ln}\:\left(\mathrm{cos}\:\alpha\right)\:−\left(\mathrm{sin}\:\alpha\right)^{\mathrm{4}} \:\mathrm{ln}\:\left(\mathrm{sin}\:\alpha\right)\: \\ $$

Answered by som(math1967) last updated on 01/May/22

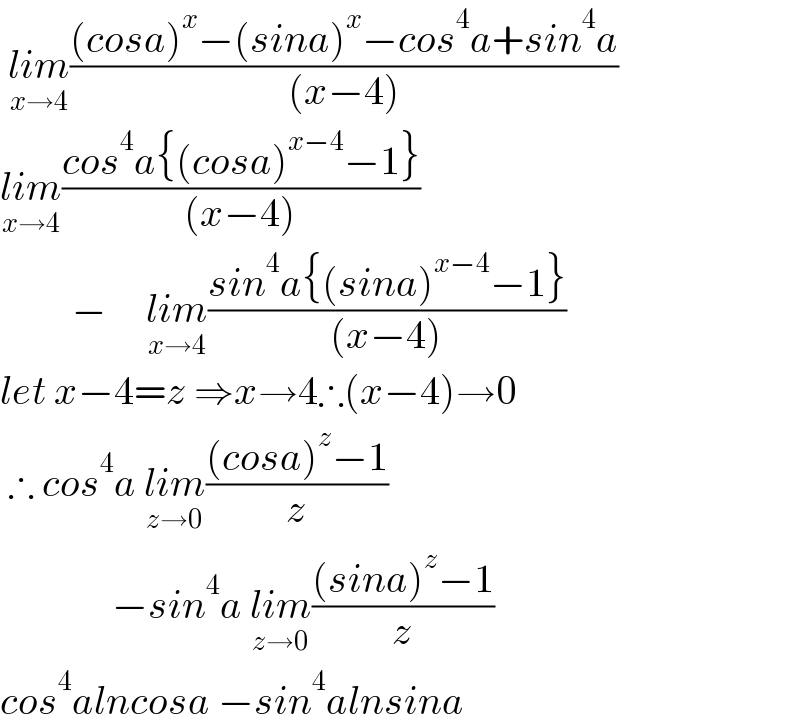
lim_(x→4) (((cosa)^x −(sina)^x −cos^4 a+sin^4 a)/((x−4))) lim_(x→4) ((cos^4 a{(cosa)^(x−4) −1})/((x−4))) − lim_(x→4) ((sin^4 a{(sina)^(x−4) −1})/((x−4))) let x−4=z ⇒x→4∴(x−4)→0 ∴ cos^4 a lim_(z→0) (((cosa)^z −1)/z) −sin^4 a lim_(z→0) (((sina)^z −1)/z) cos^4 alncosa −sin^4 alnsina

$$\:\underset{{x}\rightarrow\mathrm{4}} {{lim}}\frac{\left({cosa}\right)^{{x}} −\left({sina}\right)^{{x}} −{cos}^{\mathrm{4}} {a}+{sin}^{\mathrm{4}} {a}}{\left({x}−\mathrm{4}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{4}} {{lim}}\frac{{cos}^{\mathrm{4}} {a}\left\{\left({cosa}\right)^{{x}−\mathrm{4}} −\mathrm{1}\right\}}{\left({x}−\mathrm{4}\right)}\: \\ $$$$\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\underset{{x}\rightarrow\mathrm{4}} {{lim}}\frac{{sin}^{\mathrm{4}} {a}\left\{\left({sina}\right)^{{x}−\mathrm{4}} −\mathrm{1}\right\}}{\left({x}−\mathrm{4}\right)} \\ $$$${let}\:{x}−\mathrm{4}={z}\:\Rightarrow{x}\rightarrow\mathrm{4}\therefore\left({x}−\mathrm{4}\right)\rightarrow\mathrm{0} \\ $$$$\:\therefore\:{cos}^{\mathrm{4}} {a}\:\underset{{z}\rightarrow\mathrm{0}} {{lim}}\frac{\left({cosa}\right)^{{z}} −\mathrm{1}}{{z}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{sin}^{\mathrm{4}} {a}\:\underset{{z}\rightarrow\mathrm{0}} {{lim}}\frac{\left({sina}\right)^{{z}} −\mathrm{1}}{{z}} \\ $$$${cos}^{\mathrm{4}} {alncosa}\:−{sin}^{\mathrm{4}} {alnsina} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com