Question and Answers Forum

All Questions      Topic List

Vector Calculus Questions

Previous in All Question      Next in All Question      

Previous in Vector Calculus      

Question Number 216698 by sniper237 last updated on 16/Feb/25

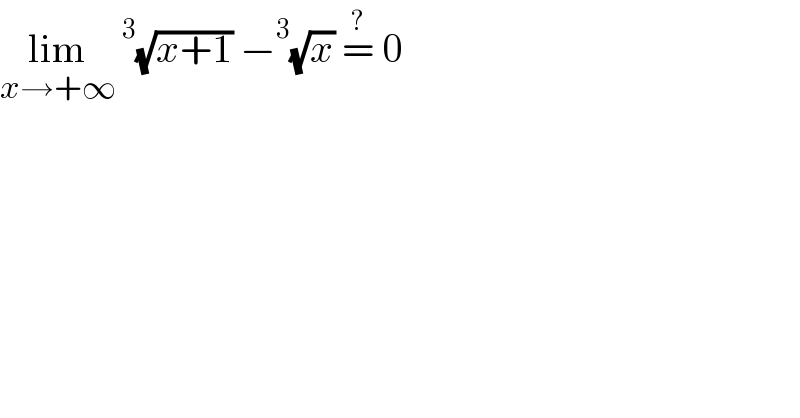
lim_(x→+∞) ^3 (√(x+1)) −^3 (√x) =^? 0

$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:^{\mathrm{3}} \sqrt{{x}+\mathrm{1}}\:−^{\mathrm{3}} \sqrt{{x}}\:\overset{?} {=}\:\mathrm{0} \\ $$

Answered by MrGaster last updated on 16/Feb/25

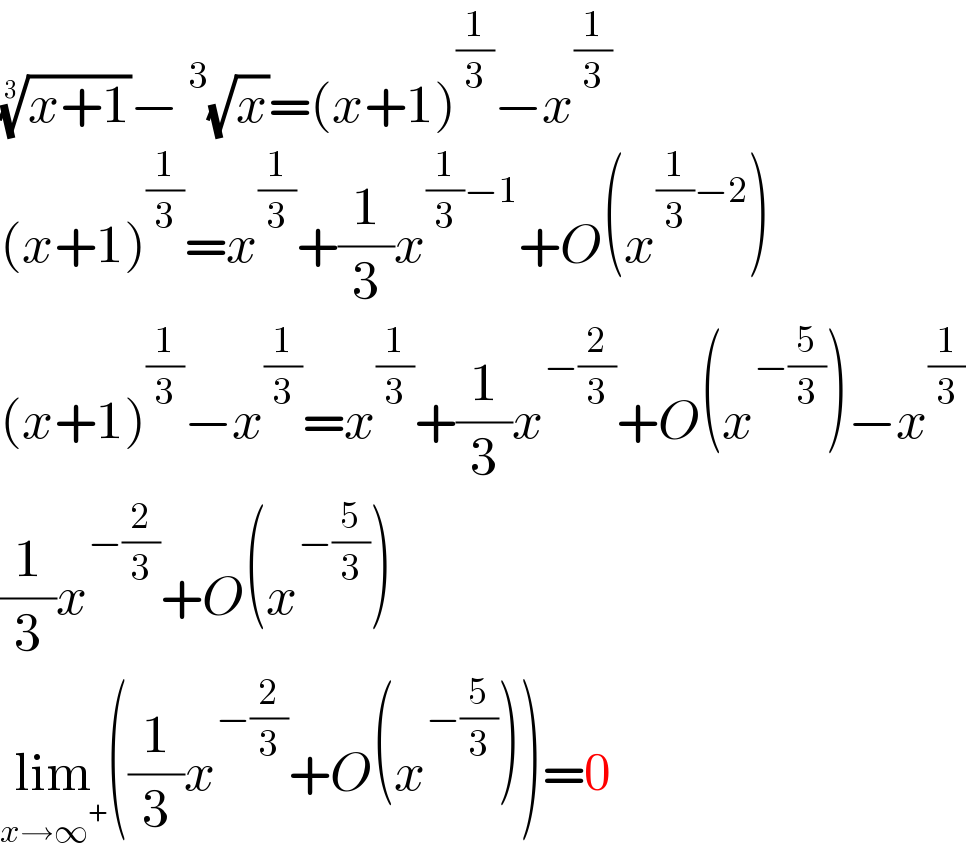
((x+1))^(1/3) −^3 (√x)=(x+1)^(1/3) −x^(1/3) (x+1)^(1/3) =x^(1/3) +(1/3)x^((1/3)−1) +O(x^((1/3)−2) ) (x+1)^(1/3) −x^(1/3) =x^(1/3) +(1/3)x^(−(2/3)) +O(x^(−(5/3)) )−x^(1/3) (1/3)x^(−(2/3)) +O(x^(−(5/3)) ) lim_(x→∞^+ ) ((1/3)x^(−(2/3)) +O(x^(−(5/3)) ))=0

$$\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}−\:^{\mathrm{3}} \sqrt{{x}}=\left({x}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −{x}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\left({x}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ={x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\frac{\mathrm{1}}{\mathrm{3}}{x}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} +{O}\left({x}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{2}} \right) \\ $$$$\left({x}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −{x}^{\frac{\mathrm{1}}{\mathrm{3}}} ={x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\frac{\mathrm{1}}{\mathrm{3}}{x}^{−\frac{\mathrm{2}}{\mathrm{3}}} +{O}\left({x}^{−\frac{\mathrm{5}}{\mathrm{3}}} \right)−{x}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{x}^{−\frac{\mathrm{2}}{\mathrm{3}}} +{O}\left({x}^{−\frac{\mathrm{5}}{\mathrm{3}}} \right) \\ $$$$\underset{{x}\rightarrow\infty^{+} } {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{3}}{x}^{−\frac{\mathrm{2}}{\mathrm{3}}} +{O}\left({x}^{−\frac{\mathrm{5}}{\mathrm{3}}} \right)\right)=\mathrm{0} \\ $$

Answered by mehdee7396 last updated on 17/Feb/25

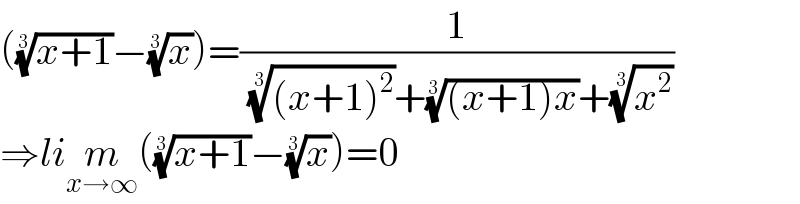
(((x+1))^(1/3) −(x)^(1/3) )=(1/( (((x+1)^2 ))^(1/3) +(((x+1)x))^(1/3) +(x^2 )^(1/3) )) ⇒lim_(x→∞) (((x+1))^(1/3) −(x)^(1/3) )=0

$$\left(\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}−\sqrt[{\mathrm{3}}]{{x}}\right)=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right){x}}+\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} }} \\ $$$$\Rightarrow{li}\underset{{x}\rightarrow\infty} {{m}}\left(\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}−\sqrt[{\mathrm{3}}]{{x}}\right)=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com