
Question Number 167943 by mathlove last updated on 30/Mar/22
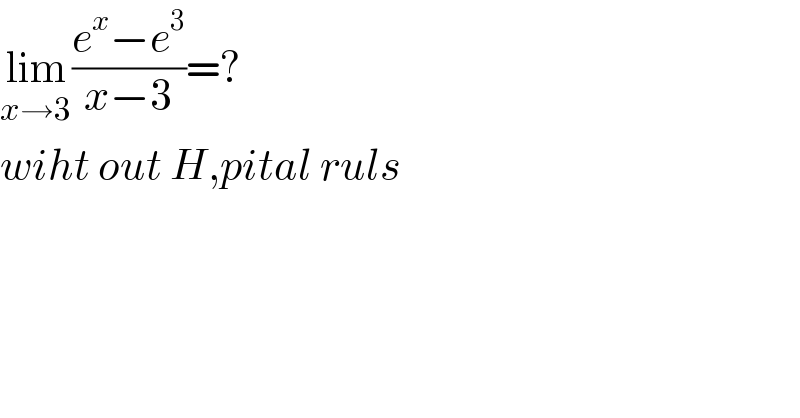
$$\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{{e}^{{x}} −{e}^{\mathrm{3}} }{{x}−\mathrm{3}}=? \\ $$$${wiht}\:{out}\:{H},{pital}\:{ruls} \\ $$
Commented by mkam last updated on 30/Mar/22
![= e^3 lim_(x→3) (([ 2 +(x−3 ) + (((x−3)^2 )/(2!)) +.....+ o(x−3)^6 ]−1)/((x−3))) = e^3 lim_(x→3) (((x−3) [1+ (((x−3))/(2!)) + ..... +o(x−3)^6 ])/((x−3))) = e^3 lim_(x→ 3 ) [1+ (((x−3))/(2!)) + ..... + o(x−3)^6 ] = e^3 ×1 = e^3 ■ alldolaimy](Q167947.png)
$$=\:\boldsymbol{{e}}^{\mathrm{3}} \:\boldsymbol{{lim}}_{\boldsymbol{{x}}\rightarrow\mathrm{3}} \:\frac{\left[\:\mathrm{2}\:+\left(\boldsymbol{{x}}−\mathrm{3}\:\right)\:+\:\frac{\left(\boldsymbol{{x}}−\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{2}!}\:+.....+\:\boldsymbol{{o}}\left(\boldsymbol{{x}}−\mathrm{3}\right)^{\mathrm{6}} \right]−\mathrm{1}}{\left(\boldsymbol{{x}}−\mathrm{3}\right)} \\ $$$$ \\ $$$$=\:\boldsymbol{{e}}^{\mathrm{3}} \:\boldsymbol{{lim}}_{\boldsymbol{{x}}\rightarrow\mathrm{3}} \:\frac{\left(\boldsymbol{{x}}−\mathrm{3}\right)\:\left[\mathrm{1}+\:\frac{\left(\boldsymbol{{x}}−\mathrm{3}\right)}{\mathrm{2}!}\:+\:.....\:+\boldsymbol{{o}}\left(\boldsymbol{{x}}−\mathrm{3}\right)^{\mathrm{6}} \:\right]}{\left(\boldsymbol{{x}}−\mathrm{3}\right)} \\ $$$$ \\ $$$$=\:\boldsymbol{{e}}^{\mathrm{3}} \:\boldsymbol{{lim}}_{\boldsymbol{{x}}\rightarrow\:\mathrm{3}\:} \:\left[\mathrm{1}+\:\frac{\left(\boldsymbol{{x}}−\mathrm{3}\right)}{\mathrm{2}!}\:+\:.....\:+\:\boldsymbol{{o}}\left(\boldsymbol{{x}}−\mathrm{3}\right)^{\mathrm{6}} \:\right]\:=\:\boldsymbol{{e}}^{\mathrm{3}} ×\mathrm{1}\:=\:\boldsymbol{{e}}^{\mathrm{3}} \\ $$$$ \\ $$$$\blacksquare\:\boldsymbol{{alldolaimy}} \\ $$
Commented by mathlove last updated on 30/Mar/22
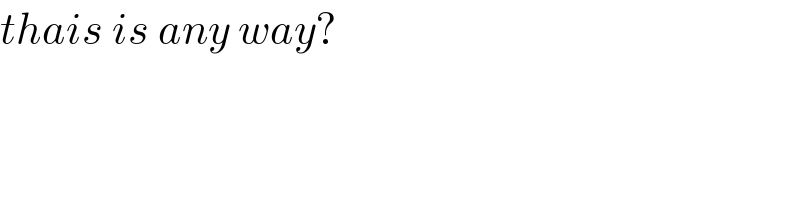
$${thais}\:{is}\:{any}\:{way}? \\ $$
Commented by mokys last updated on 30/Mar/22

$$\boldsymbol{{tylor}}\:\boldsymbol{{series}} \\ $$
Answered by alephzero last updated on 30/Mar/22
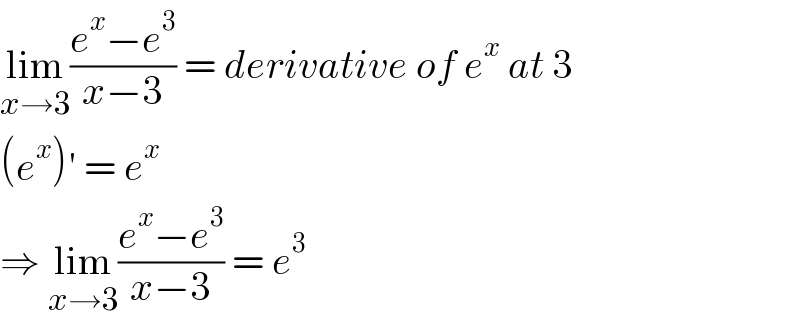
$$\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{{e}^{{x}} −{e}^{\mathrm{3}} }{{x}−\mathrm{3}}\:=\:{derivative}\:{of}\:{e}^{{x}} \:{at}\:\mathrm{3} \\ $$$$\left({e}^{{x}} \right)'\:=\:{e}^{{x}} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{{e}^{{x}} −{e}^{\mathrm{3}} }{{x}−\mathrm{3}}\:=\:{e}^{\mathrm{3}} \\ $$
Answered by 281981 last updated on 30/Mar/22
![lim((e^3 (e^(x−3) −1))/(x−3)) x−3→0 =e^3 lim((e^(x−3) −1)/(x−3)) x−3→0 =e^3 (1) [lim ((e^x −1)/x)=1 as x→0] =e^3](Q167951.png)
$${lim}\frac{{e}^{\mathrm{3}} \left({e}^{{x}−\mathrm{3}} −\mathrm{1}\right)}{{x}−\mathrm{3}} \\ $$$${x}−\mathrm{3}\rightarrow\mathrm{0} \\ $$$$={e}^{\mathrm{3}} \:{lim}\frac{{e}^{{x}−\mathrm{3}} −\mathrm{1}}{{x}−\mathrm{3}} \\ $$$${x}−\mathrm{3}\rightarrow\mathrm{0} \\ $$$$={e}^{\mathrm{3}} \left(\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{lim}\:\frac{{e}^{{x}} −\mathrm{1}}{{x}}=\mathrm{1}\:{as}\:{x}\rightarrow\mathrm{0}\right] \\ $$$$ \\ $$$$={e}^{\mathrm{3}} \\ $$
