
Question Number 114088 by bemath last updated on 17/Sep/20
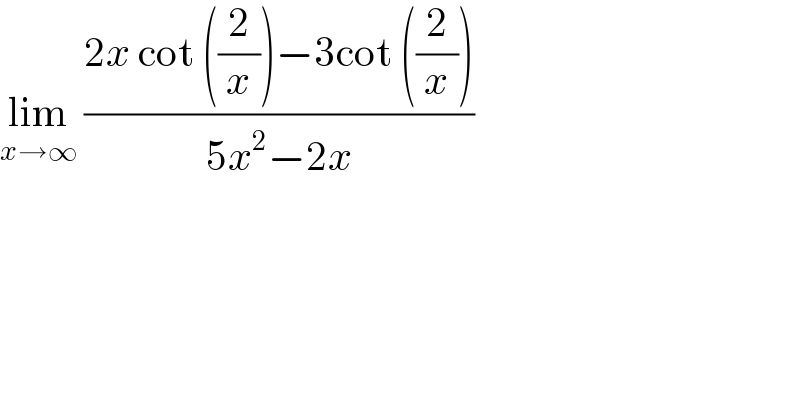
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{2}{x}\:\mathrm{cot}\:\left(\frac{\mathrm{2}}{{x}}\right)−\mathrm{3cot}\:\left(\frac{\mathrm{2}}{{x}}\right)}{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{2}{x}} \\ $$
Answered by Olaf last updated on 17/Sep/20
![= lim_(x→∞) ((1−(1/2)((2/x))^2 )/(((2/x))))[((2x−3)/(5x^2 −2x))] = lim_(x→∞) ((x^2 −2)/(2x))×((2x−3)/(5x^2 −2x)) = lim_(x→∞) ((2x^3 )/(10x^3 )) = (1/5)](Q114091.png)
$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} }{\left(\frac{\mathrm{2}}{{x}}\right)}\left[\frac{\mathrm{2}{x}−\mathrm{3}}{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{2}{x}}\right] \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{2}{x}}×\frac{\mathrm{2}{x}−\mathrm{3}}{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{2}{x}} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}{x}^{\mathrm{3}} }{\mathrm{10}{x}^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$
