Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 195154 by cortano12 last updated on 25/Jul/23

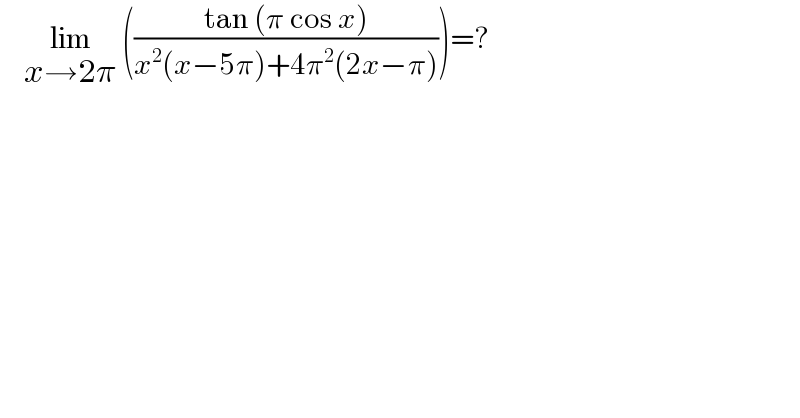
lim_(x→2π) (((tan (π cos x))/(x^2 (x−5π)+4π^2 (2x−π))))=?

$$\:\:\:\:\underset{{x}\rightarrow\mathrm{2}\pi} {\mathrm{lim}}\:\left(\frac{\mathrm{tan}\:\left(\pi\:\mathrm{cos}\:{x}\right)}{{x}^{\mathrm{2}} \left({x}−\mathrm{5}\pi\right)+\mathrm{4}\pi^{\mathrm{2}} \left(\mathrm{2}{x}−\pi\right)}\right)=? \\ $$$$ \\ $$

Answered by dimentri last updated on 25/Jul/23

x−2π=y lim_(y→0) ((tan (π cos (2π+y)))/((y+2π)^2 (y−3π)+4π^2 (2y+3π))) = lim_(y→0) ((tan (π cos y))/((y^2 +4πy+4π^2 )(y−3π)+8π^2 y+12π^3 )) = lim_(y→0) ((−tan (π(1−cos y)))/(y^3 −3πy^2 +4πy^2 −12π^2 y+4π^2 y+8π^2 y)) = lim_(y→0) ((−tan (2π sin^2 ((1/2)y)))/(y^2 (y+π))) = lim_(y→0) ((−2π sin^2 ((1/2)y))/(πy^2 )) = determinant (((−( / ))))

$$\:\: \\ $$$$\:\:{x}−\mathrm{2}\pi={y}\: \\ $$$$\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left(\pi\:\mathrm{cos}\:\left(\mathrm{2}\pi+{y}\right)\right)}{\left({y}+\mathrm{2}\pi\right)^{\mathrm{2}} \:\left({y}−\mathrm{3}\pi\right)+\mathrm{4}\pi^{\mathrm{2}} \left(\mathrm{2}{y}+\mathrm{3}\pi\right)} \\ $$$$\:=\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left(\pi\:\mathrm{cos}\:{y}\right)}{\left({y}^{\mathrm{2}} +\mathrm{4}\pi{y}+\mathrm{4}\pi^{\mathrm{2}} \right)\left({y}−\mathrm{3}\pi\right)+\mathrm{8}\pi^{\mathrm{2}} {y}+\mathrm{12}\pi^{\mathrm{3}} } \\ $$$$\:=\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{tan}\:\left(\pi\left(\mathrm{1}−\mathrm{cos}\:{y}\right)\right)}{{y}^{\mathrm{3}} −\mathrm{3}\pi{y}^{\mathrm{2}} +\mathrm{4}\pi{y}^{\mathrm{2}} −\mathrm{12}\pi^{\mathrm{2}} {y}+\mathrm{4}\pi^{\mathrm{2}} {y}+\mathrm{8}\pi^{\mathrm{2}} {y}} \\ $$$$\:=\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{tan}\:\left(\mathrm{2}\pi\:\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{y}\right)\right)}{{y}^{\mathrm{2}} \left({y}+\pi\right)} \\ $$$$\:=\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2}\pi\:\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{y}\right)}{\pi{y}^{\mathrm{2}} }\:=\:\begin{array}{|c|}{−\frac{ }{ }}\\\hline\end{array} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com