
Question Number 34007 by rahul 19 last updated on 29/Apr/18
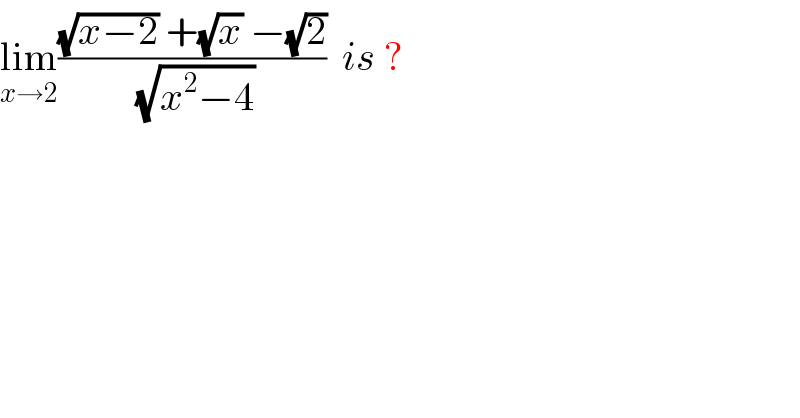
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\sqrt{{x}−\mathrm{2}}\:+\sqrt{{x}}\:−\sqrt{\mathrm{2}}}{\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}}\:\:{is}\:? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 29/Apr/18
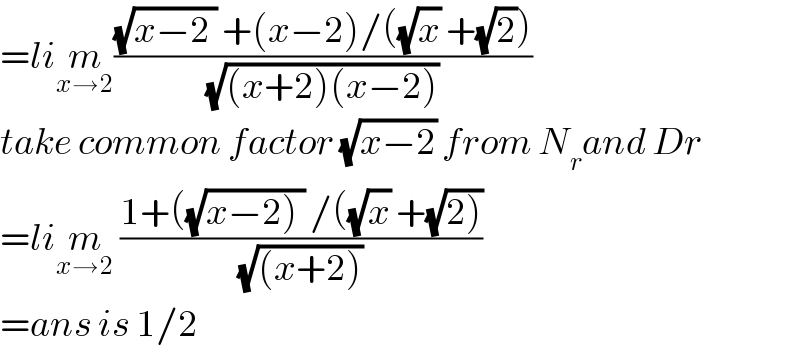
$$={li}\underset{{x}\rightarrow\mathrm{2}} {{m}}\frac{\sqrt{{x}−\mathrm{2}\:}\:+\left({x}−\mathrm{2}\right)/\left(\sqrt{{x}}\:+\sqrt{\mathrm{2}}\right)}{\sqrt{\left({x}+\mathrm{2}\right)\left({x}−\mathrm{2}\right)}\:} \\ $$$${take}\:{common}\:{factor}\:\sqrt{{x}−\mathrm{2}}\:{from}\:{N}_{{r}} {and}\:{Dr} \\ $$$$={li}\underset{{x}\rightarrow\mathrm{2}} {{m}}\:\frac{\mathrm{1}+\left(\sqrt{\left.{x}−\mathrm{2}\right)\:}\:/\left(\sqrt{{x}}\:+\sqrt{\left.\mathrm{2}\right)}\right.\right.}{\sqrt{\left({x}+\mathrm{2}\right)}\:} \\ $$$$={ans}\:{is}\:\mathrm{1}/\mathrm{2} \\ $$
Commented by rahul 19 last updated on 29/Apr/18

$$\mathscr{T}{hank}\:{you}\:{sir}. \\ $$
