Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 132483 by abdullahquwatan last updated on 14/Feb/21

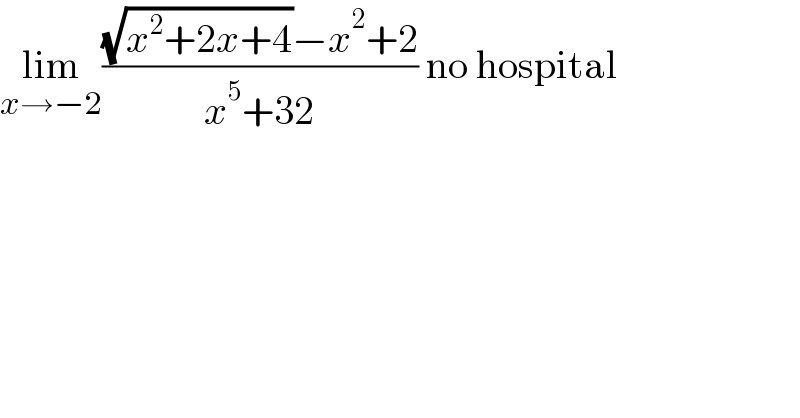
lim_(x→−2) (((√(x^2 +2x+4))−x^2 +2)/(x^5 +32)) no hospital

$$\underset{{x}\rightarrow−\mathrm{2}} {\mathrm{lim}}\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}−{x}^{\mathrm{2}} +\mathrm{2}}{{x}^{\mathrm{5}} +\mathrm{32}}\:\mathrm{no}\:\mathrm{hospital} \\ $$

Commented by EDWIN88 last updated on 14/Feb/21

what hospital?

$$\mathrm{what}\:\mathrm{hospital}? \\ $$

Commented by abdullahquwatan last updated on 14/Feb/21

l′hopital theorem

$$\mathrm{l}'\mathrm{hopital}\:\mathrm{theorem} \\ $$

Answered by EDWIN88 last updated on 14/Feb/21

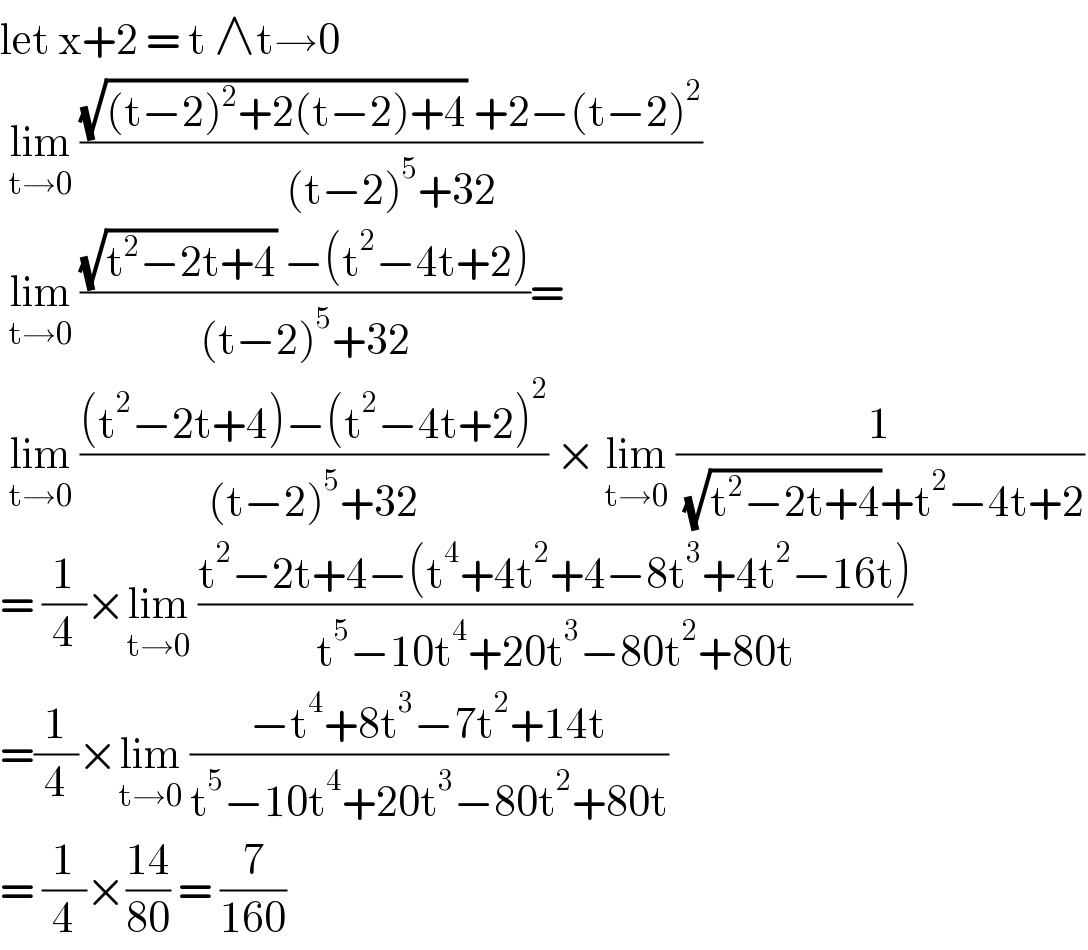
let x+2 = t ∧t→0 lim_(t→0) (((√((t−2)^2 +2(t−2)+4)) +2−(t−2)^2 )/((t−2)^5 +32)) lim_(t→0) (((√(t^2 −2t+4)) −(t^2 −4t+2))/((t−2)^5 +32))= lim_(t→0) (((t^2 −2t+4)−(t^2 −4t+2)^2 )/((t−2)^5 +32)) × lim_(t→0) (1/( (√(t^2 −2t+4))+t^2 −4t+2)) = (1/4)×lim_(t→0) ((t^2 −2t+4−(t^4 +4t^2 +4−8t^3 +4t^2 −16t))/(t^5 −10t^4 +20t^3 −80t^2 +80t)) =(1/4)×lim_(t→0) ((−t^4 +8t^3 −7t^2 +14t)/(t^5 −10t^4 +20t^3 −80t^2 +80t)) = (1/4)×((14)/(80)) = (7/(160))

$$\mathrm{let}\:\mathrm{x}+\mathrm{2}\:=\:\mathrm{t}\:\wedge\mathrm{t}\rightarrow\mathrm{0} \\ $$$$\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\left(\mathrm{t}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{t}−\mathrm{2}\right)+\mathrm{4}}\:+\mathrm{2}−\left(\mathrm{t}−\mathrm{2}\right)^{\mathrm{2}} }{\left(\mathrm{t}−\mathrm{2}\right)^{\mathrm{5}} +\mathrm{32}} \\ $$$$\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{2t}+\mathrm{4}}\:−\left(\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{2}\right)}{\left(\mathrm{t}−\mathrm{2}\right)^{\mathrm{5}} +\mathrm{32}}= \\ $$$$\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2t}+\mathrm{4}\right)−\left(\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{2}\right)^{\mathrm{2}} }{\left(\mathrm{t}−\mathrm{2}\right)^{\mathrm{5}} +\mathrm{32}}\:×\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{2t}+\mathrm{4}}+\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{2}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}×\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{2t}+\mathrm{4}−\left(\mathrm{t}^{\mathrm{4}} +\mathrm{4t}^{\mathrm{2}} +\mathrm{4}−\mathrm{8t}^{\mathrm{3}} +\mathrm{4t}^{\mathrm{2}} −\mathrm{16t}\right)}{\mathrm{t}^{\mathrm{5}} −\mathrm{10t}^{\mathrm{4}} +\mathrm{20t}^{\mathrm{3}} −\mathrm{80t}^{\mathrm{2}} +\mathrm{80t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}×\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{t}^{\mathrm{4}} +\mathrm{8t}^{\mathrm{3}} −\mathrm{7t}^{\mathrm{2}} +\mathrm{14t}}{\mathrm{t}^{\mathrm{5}} −\mathrm{10t}^{\mathrm{4}} +\mathrm{20t}^{\mathrm{3}} −\mathrm{80t}^{\mathrm{2}} +\mathrm{80t}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{14}}{\mathrm{80}}\:=\:\frac{\mathrm{7}}{\mathrm{160}} \\ $$

Commented by abdullahquwatan last updated on 14/Feb/21

thank you so much

$${thank}\:{you}\:{so}\:{much} \\ $$

Answered by bemath last updated on 14/Feb/21

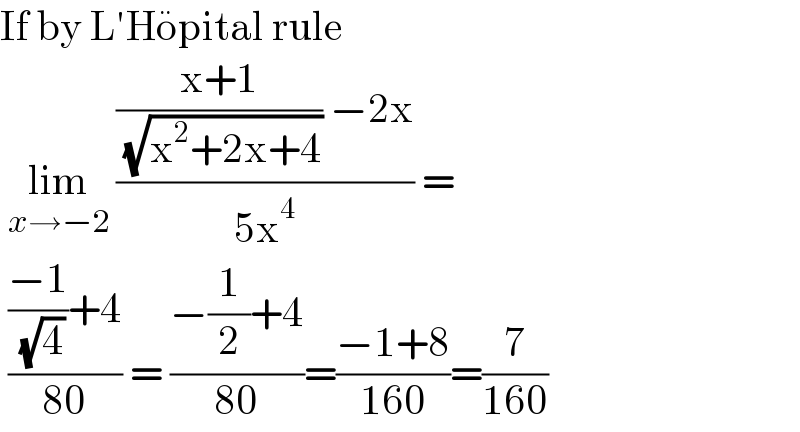
If by L′Ho^ pital rule lim_(x→−2) ((((x+1)/( (√(x^2 +2x+4)))) −2x)/(5x^4 )) = ((((−1)/( (√4)))+4)/(80)) = ((−(1/2)+4)/(80))=((−1+8)/(160))=(7/(160))

$$\mathrm{If}\:\mathrm{by}\:\mathrm{L}'\mathrm{H}\ddot {\mathrm{o}pital}\:\mathrm{rule} \\ $$$$\:\underset{{x}\rightarrow−\mathrm{2}} {\mathrm{lim}}\:\frac{\frac{\mathrm{x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{4}}}\:−\mathrm{2x}}{\mathrm{5x}^{\mathrm{4}} }\:= \\ $$$$\:\frac{\frac{−\mathrm{1}}{\:\sqrt{\mathrm{4}}}+\mathrm{4}}{\mathrm{80}}\:=\:\frac{−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{4}}{\mathrm{80}}=\frac{−\mathrm{1}+\mathrm{8}}{\mathrm{160}}=\frac{\mathrm{7}}{\mathrm{160}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com