Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 167663 by mathlove last updated on 22/Mar/22

lim_(x→2) [log((1/x)+(1/(2x))+(1/(4x)).......)]=?

$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\left[{log}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{4}{x}}.......\right)\right]=? \\ $$

Commented by mathlove last updated on 22/Mar/22

????

$$???? \\ $$

Commented by alephzero last updated on 22/Mar/22

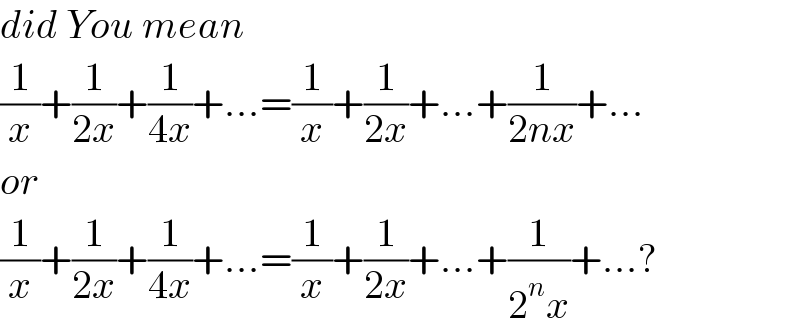
did You mean (1/x)+(1/(2x))+(1/(4x))+...=(1/x)+(1/(2x))+...+(1/(2nx))+... or (1/x)+(1/(2x))+(1/(4x))+...=(1/x)+(1/(2x))+...+(1/(2^n x))+...?

$${did}\:{You}\:{mean}\: \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{4}{x}}+...=\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}{x}}+...+\frac{\mathrm{1}}{\mathrm{2}{nx}}+... \\ $$$${or} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{4}{x}}+...=\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}{x}}+...+\frac{\mathrm{1}}{\mathrm{2}^{{n}} {x}}+...? \\ $$

Answered by alephzero last updated on 22/Mar/22

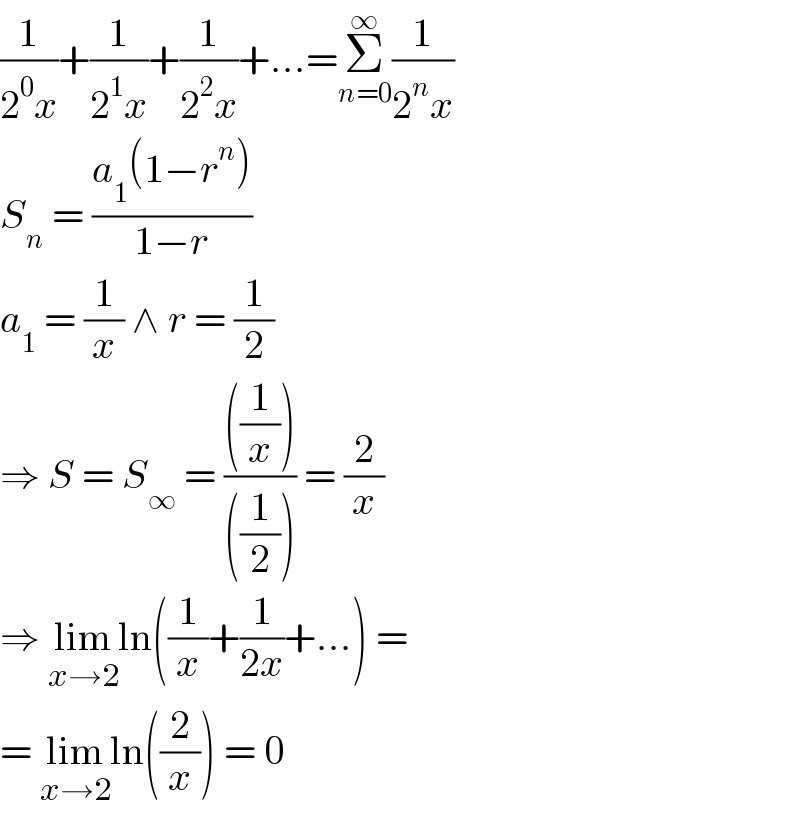
(1/(2^0 x))+(1/(2^1 x))+(1/(2^2 x))+...=Σ_(n=0) ^∞ (1/(2^n x)) S_n = ((a_1 (1−r^n ))/(1−r)) a_1 = (1/x) ∧ r = (1/2) ⇒ S = S_∞ = ((((1/x)))/(((1/2)))) = (2/x) ⇒ lim_(x→2) ln((1/x)+(1/(2x))+...) = = lim_(x→2) ln((2/x)) = 0

$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} {x}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} {x}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} {x}}+...=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {x}} \\ $$$${S}_{{n}} \:=\:\frac{{a}_{\mathrm{1}} \left(\mathrm{1}−{r}^{{n}} \right)}{\mathrm{1}−{r}} \\ $$$${a}_{\mathrm{1}} \:=\:\frac{\mathrm{1}}{{x}}\:\wedge\:{r}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:{S}\:=\:{S}_{\infty} \:=\:\frac{\left(\frac{\mathrm{1}}{{x}}\right)}{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=\:\frac{\mathrm{2}}{{x}} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}ln}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}{x}}+...\right)\:= \\ $$$$=\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}ln}\left(\frac{\mathrm{2}}{{x}}\right)\:=\:\mathrm{0} \\ $$

Commented by mathlove last updated on 22/Mar/22

thanks sir

$${thanks}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com