Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 203980 by Davidtim last updated on 03/Feb/24

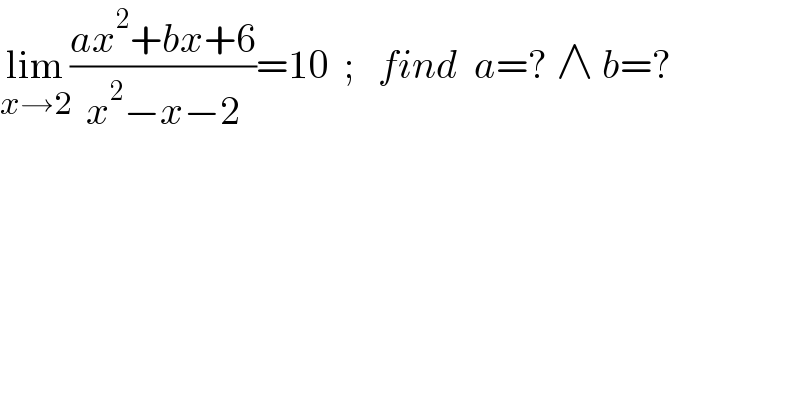
lim_(x→2) ((ax^2 +bx+6)/(x^2 −x−2))=10 ; find a=? ∧ b=?

$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{ax}^{\mathrm{2}} +{bx}+\mathrm{6}}{{x}^{\mathrm{2}} −{x}−\mathrm{2}}=\mathrm{10}\:\:;\:\:\:{find}\:\:{a}=?\:\wedge\:{b}=? \\ $$

Answered by deleteduser1 last updated on 03/Feb/24

((a(x^2 −x−2)+(b+a)x+6+2a)/(x^2 −x−2))=10 ⇒lim_(x→2) [a+(((b+a)x+6+2a)/((x−2)(x+1)))]=10 ⇒lim_(x→2) (((b+a)x+6+2a)/((x−2)(x+1)))=10−a 2(b+a)+6+2a=0⇒2a+b=−3 ...(i) ⇒lim_(x→2) (((b+a)x+6+2a)/((x−2)(x+1)))=lim_(x→2) ((b+a)/(2x−1))=((b+a)/3)=10−a ⇒b+a=30−3a⇒4a+b=30...(ii) (i)∧(ii)⇒a=16.5⇒b=−36

$$\frac{{a}\left({x}^{\mathrm{2}} −{x}−\mathrm{2}\right)+\left({b}+{a}\right){x}+\mathrm{6}+\mathrm{2}{a}}{{x}^{\mathrm{2}} −{x}−\mathrm{2}}=\mathrm{10} \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{2}} {{lim}}\left[{a}+\frac{\left({b}+{a}\right){x}+\mathrm{6}+\mathrm{2}{a}}{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)}\right]=\mathrm{10} \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{2}} {{lim}}\frac{\left({b}+{a}\right){x}+\mathrm{6}+\mathrm{2}{a}}{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)}=\mathrm{10}−{a} \\ $$$$\mathrm{2}\left({b}+{a}\right)+\mathrm{6}+\mathrm{2}{a}=\mathrm{0}\Rightarrow\mathrm{2}{a}+{b}=−\mathrm{3}\:...\left({i}\right) \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{2}} {{lim}}\frac{\left({b}+{a}\right){x}+\mathrm{6}+\mathrm{2}{a}}{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)}=\underset{{x}\rightarrow\mathrm{2}} {{lim}}\frac{{b}+{a}}{\mathrm{2}{x}−\mathrm{1}}=\frac{{b}+{a}}{\mathrm{3}}=\mathrm{10}−{a} \\ $$$$\Rightarrow{b}+{a}=\mathrm{30}−\mathrm{3}{a}\Rightarrow\mathrm{4}{a}+{b}=\mathrm{30}...\left({ii}\right) \\ $$$$\left({i}\right)\wedge\left({ii}\right)\Rightarrow{a}=\mathrm{16}.\mathrm{5}\Rightarrow{b}=−\mathrm{36} \\ $$

Answered by mr W last updated on 03/Feb/24

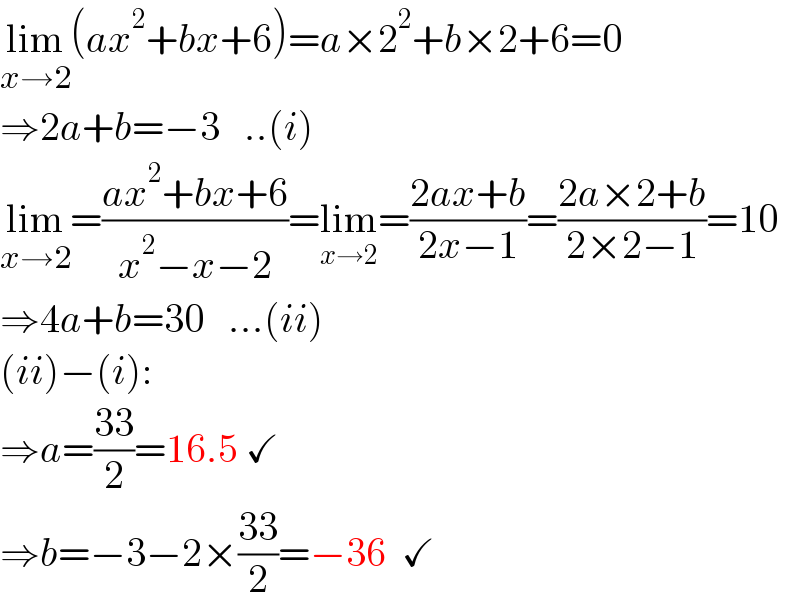
lim_(x→2) (ax^2 +bx+6)=a×2^2 +b×2+6=0 ⇒2a+b=−3 ..(i) lim_(x→2) =((ax^2 +bx+6)/(x^2 −x−2))=lim_(x→2) =((2ax+b)/(2x−1))=((2a×2+b)/(2×2−1))=10 ⇒4a+b=30 ...(ii) (ii)−(i): ⇒a=((33)/2)=16.5 ✓ ⇒b=−3−2×((33)/2)=−36 ✓

$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\left({ax}^{\mathrm{2}} +{bx}+\mathrm{6}\right)={a}×\mathrm{2}^{\mathrm{2}} +{b}×\mathrm{2}+\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{a}+{b}=−\mathrm{3}\:\:\:..\left({i}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}=\frac{{ax}^{\mathrm{2}} +{bx}+\mathrm{6}}{{x}^{\mathrm{2}} −{x}−\mathrm{2}}=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}=\frac{\mathrm{2}{ax}+{b}}{\mathrm{2}{x}−\mathrm{1}}=\frac{\mathrm{2}{a}×\mathrm{2}+{b}}{\mathrm{2}×\mathrm{2}−\mathrm{1}}=\mathrm{10} \\ $$$$\Rightarrow\mathrm{4}{a}+{b}=\mathrm{30}\:\:\:...\left({ii}\right) \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$$\Rightarrow{a}=\frac{\mathrm{33}}{\mathrm{2}}=\mathrm{16}.\mathrm{5}\:\checkmark \\ $$$$\Rightarrow{b}=−\mathrm{3}−\mathrm{2}×\frac{\mathrm{33}}{\mathrm{2}}=−\mathrm{36}\:\:\checkmark \\ $$

Commented by esmaeil last updated on 03/Feb/24

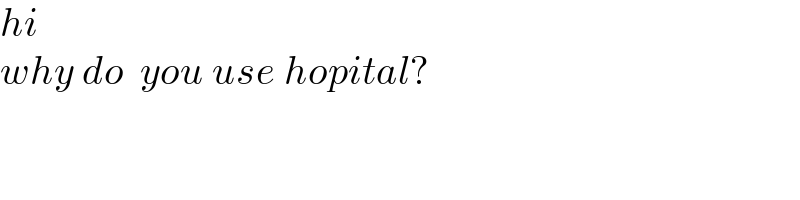
hi why do you use hopital?

$${hi} \\ $$$${why}\:{do}\:\:{you}\:{use}\:{hopital}? \\ $$

Commented by mr W last updated on 03/Feb/24

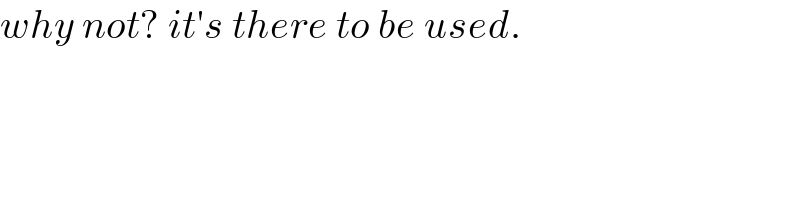
why not? it′s there to be used.

$${why}\:{not}?\:{it}'{s}\:{there}\:{to}\:{be}\:{used}. \\ $$

Commented by esmaeil last updated on 03/Feb/24

ax^2 +bx+6]_(x=2) =^(??) 0

$$\left.{ax}^{\mathrm{2}} +{bx}+\mathrm{6}\right]_{{x}=\mathrm{2}} \overset{??} {=}\mathrm{0} \\ $$

Commented by mr W last updated on 03/Feb/24

such that limit exists, ax^2 +bx+6]_(x=2) =^(must) 0. otherwise lim_(x→2) ((ax^2 +bx+6)/(x^2 −x−2))=∞

$${such}\:{that}\:{limit}\:{exists}, \\ $$$$\left.{ax}^{\mathrm{2}} +{bx}+\mathrm{6}\right]_{{x}=\mathrm{2}} \overset{{must}} {=}\mathrm{0}.\:{otherwise} \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{ax}^{\mathrm{2}} +{bx}+\mathrm{6}}{{x}^{\mathrm{2}} −{x}−\mathrm{2}}=\infty \\ $$

Commented by esmaeil last updated on 03/Feb/24

⋛

$$\:\underline{\underbrace{\lesseqgtr}} \\ $$

Commented by Mathspace last updated on 03/Feb/24

sir smael hospital is good in this case...

$${sir}\:{smael}\:{hospital}\:{is}\:{good}\:{in}\:{this}\:{case}... \\ $$

Commented by esmaeil last updated on 03/Feb/24

ok. thanks. which is right? hopital or hospital.?

$${ok}. \\ $$$${thanks}. \\ $$$${which}\:\:{is}\:\:{right}? \\ $$$${hopital}\:{or}\:{hospital}.? \\ $$

Commented by mr W last updated on 03/Feb/24

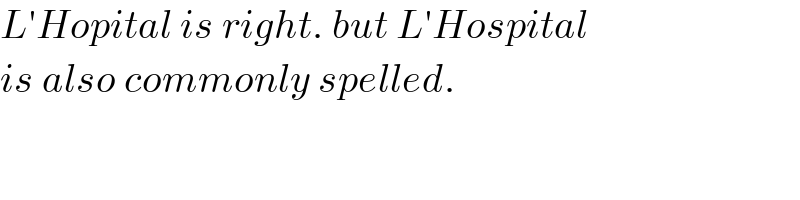
L′Hopital is right. but L′Hospital is also commonly spelled.

$${L}'{Hopital}\:{is}\:{right}.\:{but}\:{L}'{Hospital} \\ $$$${is}\:{also}\:{commonly}\:{spelled}. \\ $$

Commented by siyathokoza last updated on 07/Feb/24

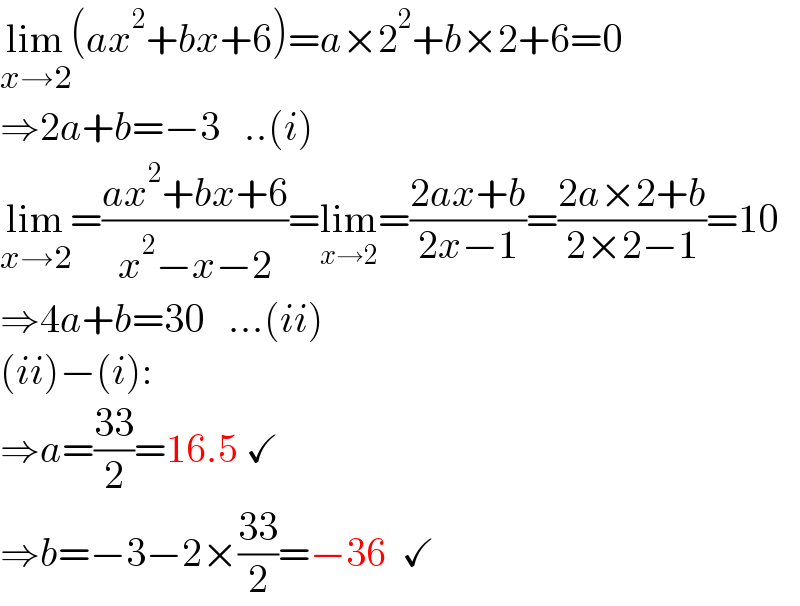
lim_(x→2) (ax^2 +bx+6)=a×2^2 +b×2+6=0 ⇒2a+b=−3 ..(i) lim_(x→2) =((ax^2 +bx+6)/(x^2 −x−2))=lim_(x→2) =((2ax+b)/(2x−1))=((2a×2+b)/(2×2−1))=10 ⇒4a+b=30 ...(ii) (ii)−(i): ⇒a=((33)/2)=16.5 ✓ ⇒b=−3−2×((33)/2)=−36 ✓

$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\left({ax}^{\mathrm{2}} +{bx}+\mathrm{6}\right)={a}×\mathrm{2}^{\mathrm{2}} +{b}×\mathrm{2}+\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{a}+{b}=−\mathrm{3}\:\:\:..\left({i}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}=\frac{{ax}^{\mathrm{2}} +{bx}+\mathrm{6}}{{x}^{\mathrm{2}} −{x}−\mathrm{2}}=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}=\frac{\mathrm{2}{ax}+{b}}{\mathrm{2}{x}−\mathrm{1}}=\frac{\mathrm{2}{a}×\mathrm{2}+{b}}{\mathrm{2}×\mathrm{2}−\mathrm{1}}=\mathrm{10} \\ $$$$\Rightarrow\mathrm{4}{a}+{b}=\mathrm{30}\:\:\:...\left({ii}\right) \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$$\Rightarrow{a}=\frac{\mathrm{33}}{\mathrm{2}}=\mathrm{16}.\mathrm{5}\:\checkmark \\ $$$$\Rightarrow{b}=−\mathrm{3}−\mathrm{2}×\frac{\mathrm{33}}{\mathrm{2}}=−\mathrm{36}\:\:\checkmark \\ $$

Commented by mr W last updated on 07/Feb/24

does it make any sense that you post a copy from other people′s workings?

$${does}\:{it}\:{make}\:{any}\:{sense}\:{that}\:{you}\: \\ $$$${post}\:{a}\:{copy}\:{from}\:{other}\:{people}'{s} \\ $$$${workings}? \\ $$

Answered by Rasheed.Sindhi last updated on 03/Feb/24

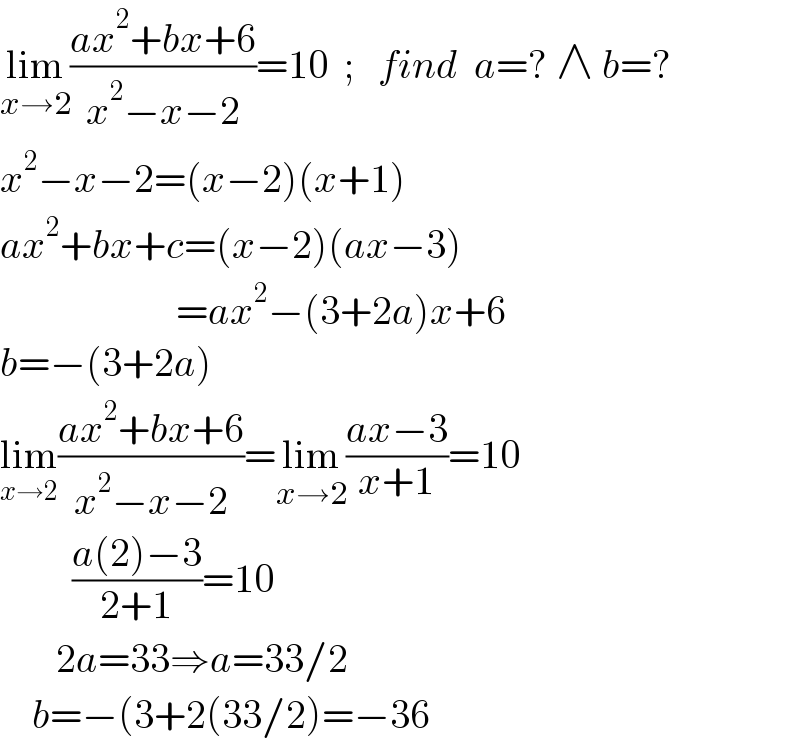
lim_(x→2) ((ax^2 +bx+6)/(x^2 −x−2))=10 ; find a=? ∧ b=? x^2 −x−2=(x−2)(x+1) ax^2 +bx+c=(x−2)(ax−3) =ax^2 −(3+2a)x+6 b=−(3+2a) lim_(x→2) ((ax^2 +bx+6)/(x^2 −x−2))=lim_(x→2) ((ax−3)/(x+1))=10 ((a(2)−3)/(2+1))=10 2a=33⇒a=33/2 b=−(3+2(33/2)=−36

$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{ax}^{\mathrm{2}} +{bx}+\mathrm{6}}{{x}^{\mathrm{2}} −{x}−\mathrm{2}}=\mathrm{10}\:\:;\:\:\:{find}\:\:{a}=?\:\wedge\:{b}=? \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{2}=\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right) \\ $$$${ax}^{\mathrm{2}} +{bx}+{c}=\left({x}−\mathrm{2}\right)\left({ax}−\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={ax}^{\mathrm{2}} −\left(\mathrm{3}+\mathrm{2}{a}\right){x}+\mathrm{6} \\ $$$${b}=−\left(\mathrm{3}+\mathrm{2}{a}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{ax}^{\mathrm{2}} +{bx}+\mathrm{6}}{{x}^{\mathrm{2}} −{x}−\mathrm{2}}=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{ax}−\mathrm{3}}{{x}+\mathrm{1}}=\mathrm{10} \\ $$$$\:\:\:\:\:\:\:\:\:\frac{{a}\left(\mathrm{2}\right)−\mathrm{3}}{\mathrm{2}+\mathrm{1}}=\mathrm{10} \\ $$$$\:\:\:\:\:\:\:\mathrm{2}{a}=\mathrm{33}\Rightarrow{a}=\mathrm{33}/\mathrm{2} \\ $$$$\:\:\:\:{b}=−\left(\mathrm{3}+\mathrm{2}\left(\mathrm{33}/\mathrm{2}\right)=−\mathrm{36}\right. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com