Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 193532 by horsebrand11 last updated on 16/Jun/23

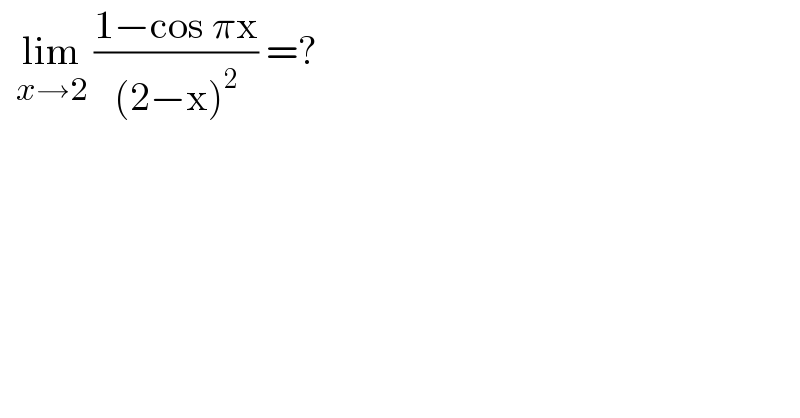
lim_(x→2) ((1−cos πx)/((2−x)^2 )) =?

$$\:\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\pi\mathrm{x}}{\left(\mathrm{2}−\mathrm{x}\right)^{\mathrm{2}} }\:=? \\ $$

Answered by aba last updated on 16/Jun/23

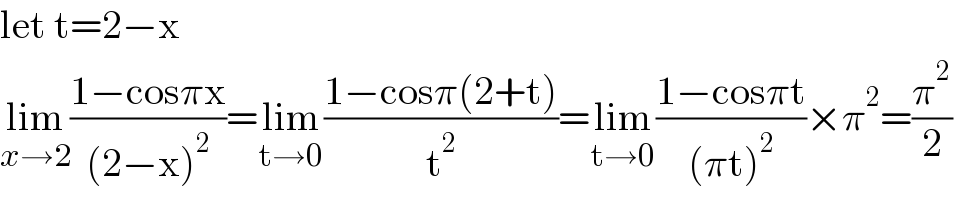
let t=2−x lim_(x→2) ((1−cosπx)/((2−x)^2 ))=lim_(t→0) ((1−cosπ(2+t))/t^2 )=lim_(t→0) ((1−cosπt)/((πt)^2 ))×π^2 =(π^2 /2)

$$\mathrm{let}\:\mathrm{t}=\mathrm{2}−\mathrm{x} \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\pi\mathrm{x}}{\left(\mathrm{2}−\mathrm{x}\right)^{\mathrm{2}} }=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\pi\left(\mathrm{2}+\mathrm{t}\right)}{\mathrm{t}^{\mathrm{2}} }=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\pi\mathrm{t}}{\left(\pi\mathrm{t}\right)^{\mathrm{2}} }×\pi^{\mathrm{2}} =\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$

Answered by cortano12 last updated on 16/Jun/23

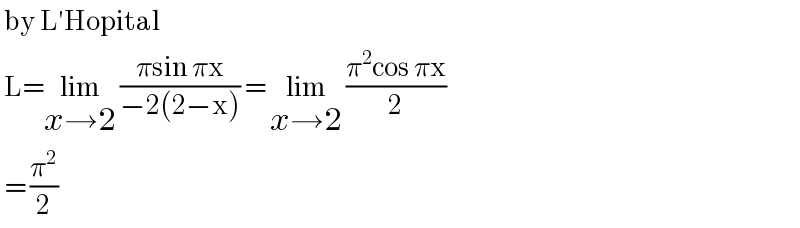
by L′Hopital L=lim_(x→2) ((πsin πx)/(−2(2−x))) = lim_(x→2) ((π^2 cos πx)/2) = (π^2 /2)

$$\:\mathrm{by}\:\mathrm{L}'\mathrm{Hopital}\: \\ $$$$\:\mathrm{L}=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\pi\mathrm{sin}\:\pi\mathrm{x}}{−\mathrm{2}\left(\mathrm{2}−\mathrm{x}\right)}\:=\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\pi^{\mathrm{2}} \mathrm{cos}\:\pi\mathrm{x}}{\mathrm{2}} \\ $$$$\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com