
Question Number 187983 by TUN last updated on 24/Feb/23
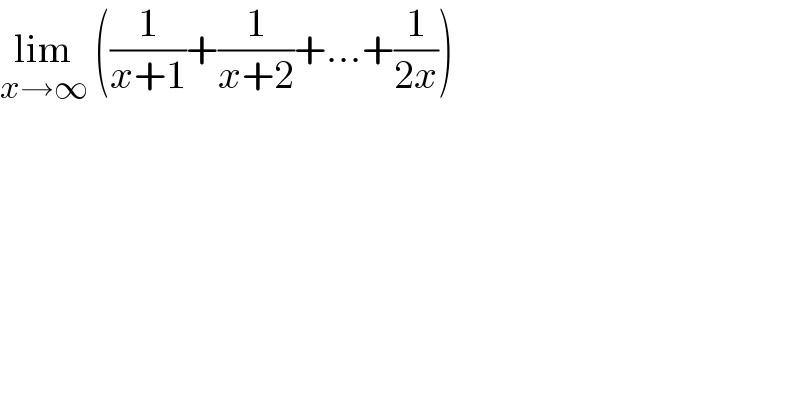
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{{x}+\mathrm{2}}+...+\frac{\mathrm{1}}{\mathrm{2}{x}}\right) \\ $$
Answered by cortano12 last updated on 24/Feb/23
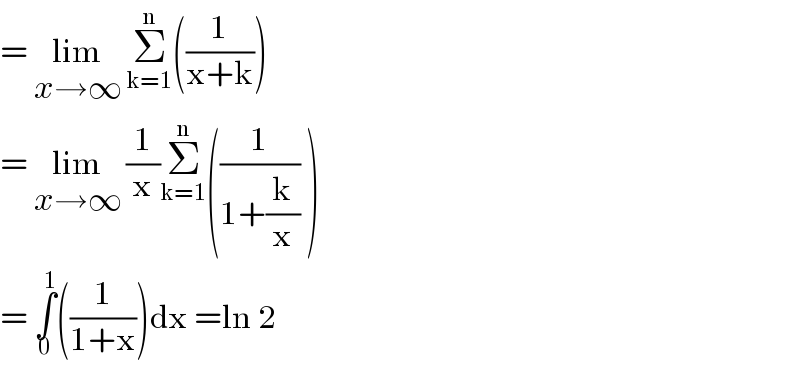
$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{x}+\mathrm{k}}\right) \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{x}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{k}}{\mathrm{x}}}\:\right) \\ $$$$=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\right)\mathrm{dx}\:=\mathrm{ln}\:\mathrm{2}\: \\ $$
Commented by Ar Brandon last updated on 24/Feb/23

$$\underset{{k}=\mathrm{1}} {\overset{{x}} {\sum}} \\ $$
