Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 132328 by liberty last updated on 13/Feb/21

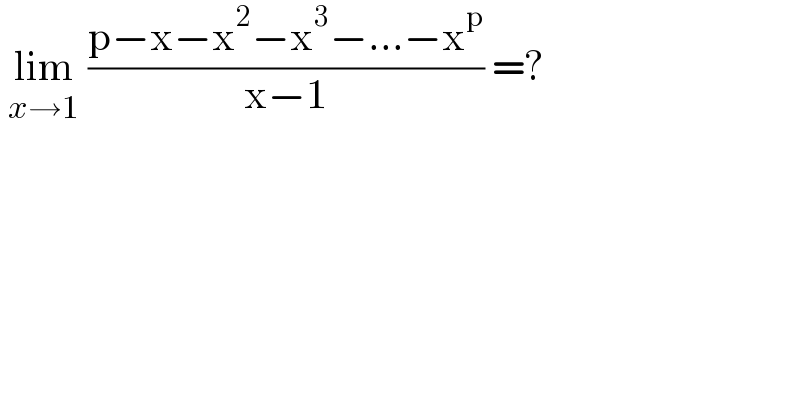
lim_(x→1) ((p−x−x^2 −x^3 −...−x^p )/(x−1)) =?

$$\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{p}−\mathrm{x}−\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{3}} −...−\mathrm{x}^{\mathrm{p}} }{\mathrm{x}−\mathrm{1}}\:=? \\ $$

Answered by EDWIN88 last updated on 13/Feb/21

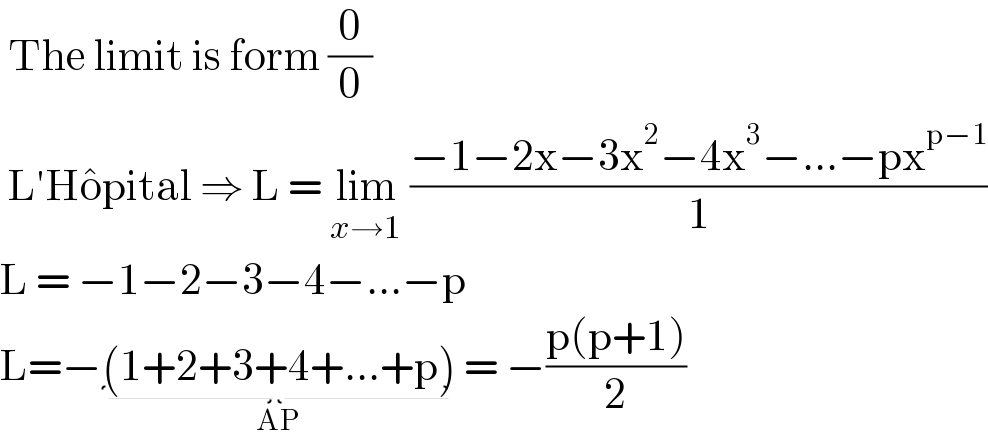
The limit is form (0/0) L′Ho^� pital ⇒ L = lim_(x→1) ((−1−2x−3x^2 −4x^3 −...−px^(p−1) )/1) L = −1−2−3−4−...−p L=−(1+2+3+4+...+p)_(AP) = −((p(p+1))/2)

$$\:\mathrm{The}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{form}\:\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\:\mathrm{L}'\mathrm{H}\hat {\mathrm{o}pital}\:\Rightarrow\:\mathrm{L}\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{−\mathrm{1}−\mathrm{2x}−\mathrm{3x}^{\mathrm{2}} −\mathrm{4x}^{\mathrm{3}} −...−\mathrm{px}^{\mathrm{p}−\mathrm{1}} }{\mathrm{1}} \\ $$$$\mathrm{L}\:=\:−\mathrm{1}−\mathrm{2}−\mathrm{3}−\mathrm{4}−...−\mathrm{p} \\ $$$$\mathrm{L}=−\underset{\mathrm{AP}} {\underbrace{\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+...+\mathrm{p}\right)}}\:=\:−\frac{\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)}{\mathrm{2}} \\ $$

Answered by mathmax by abdo last updated on 13/Feb/21

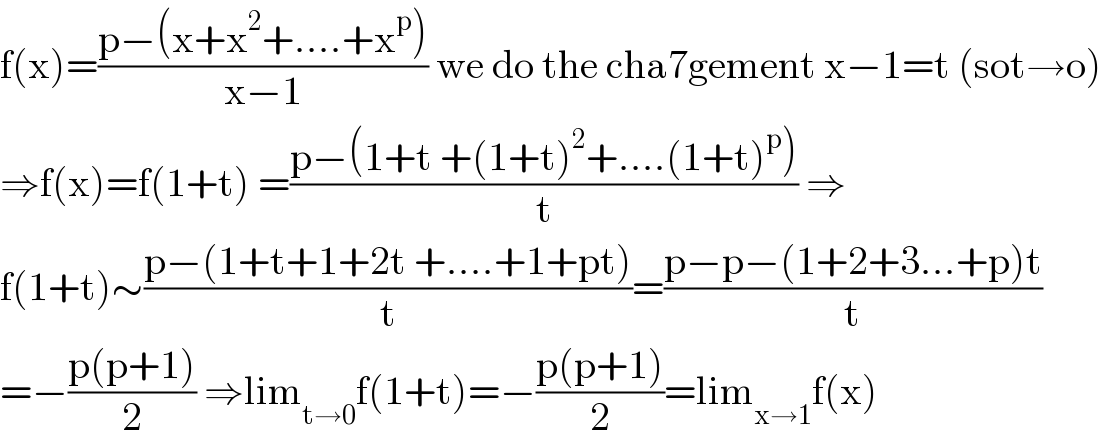
f(x)=((p−(x+x^2 +....+x^p ))/(x−1)) we do the cha7gement x−1=t (sot→o) ⇒f(x)=f(1+t) =((p−(1+t +(1+t)^2 +....(1+t)^p ))/t) ⇒ f(1+t)∼((p−(1+t+1+2t +....+1+pt))/t)=((p−p−(1+2+3...+p)t)/t) =−((p(p+1))/2) ⇒lim_(t→0) f(1+t)=−((p(p+1))/2)=lim_(x→1) f(x)

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{p}−\left(\mathrm{x}+\mathrm{x}^{\mathrm{2}} +....+\mathrm{x}^{\mathrm{p}} \right)}{\mathrm{x}−\mathrm{1}}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{cha7gement}\:\mathrm{x}−\mathrm{1}=\mathrm{t}\:\left(\mathrm{sot}\rightarrow\mathrm{o}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{1}+\mathrm{t}\right)\:=\frac{\mathrm{p}−\left(\mathrm{1}+\mathrm{t}\:+\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} +....\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{p}} \right)}{\mathrm{t}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{1}+\mathrm{t}\right)\sim\frac{\mathrm{p}−\left(\mathrm{1}+\mathrm{t}+\mathrm{1}+\mathrm{2t}\:+....+\mathrm{1}+\mathrm{pt}\right)}{\mathrm{t}}=\frac{\mathrm{p}−\mathrm{p}−\left(\mathrm{1}+\mathrm{2}+\mathrm{3}...+\mathrm{p}\right)\mathrm{t}}{\mathrm{t}} \\ $$$$=−\frac{\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)}{\mathrm{2}}\:\Rightarrow\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{1}+\mathrm{t}\right)=−\frac{\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)}{\mathrm{2}}=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com