Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 184773 by Ml last updated on 11/Jan/23

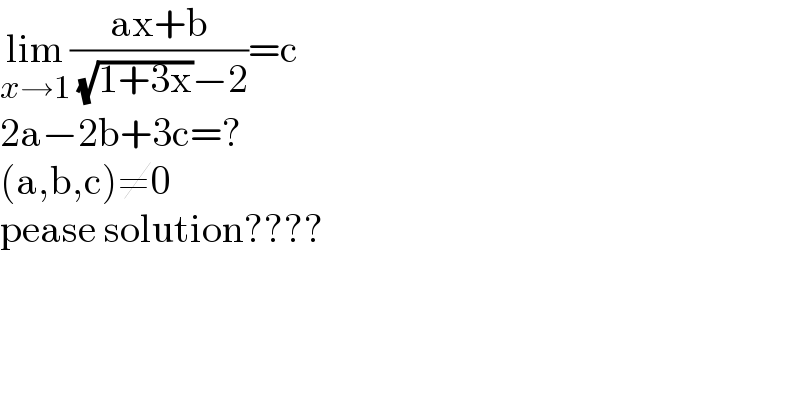
lim_(x→1) ((ax+b)/( (√(1+3x))−2))=c 2a−2b+3c=? (a,b,c)≠0 pease solution????

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{ax}+\mathrm{b}}{\:\sqrt{\mathrm{1}+\mathrm{3x}}−\mathrm{2}}=\mathrm{c} \\ $$$$\mathrm{2a}−\mathrm{2b}+\mathrm{3c}=? \\ $$$$\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)\neq\mathrm{0} \\ $$$$\mathrm{pease}\:\mathrm{solution}???? \\ $$

Commented by SEKRET last updated on 11/Jan/23

2a−2b− 3c =0

$$\:\mathrm{2}\boldsymbol{\mathrm{a}}−\mathrm{2}\boldsymbol{\mathrm{b}}−\:\mathrm{3}\boldsymbol{\mathrm{c}}\:=\mathrm{0} \\ $$

Answered by SEKRET last updated on 11/Jan/23

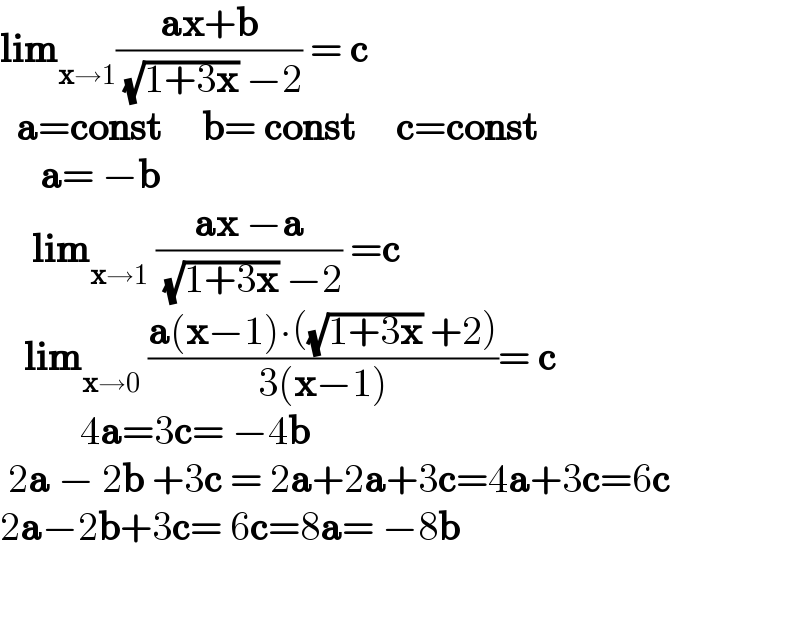
lim_(x→1) ((ax+b)/( (√(1+3x)) −2)) = c a=const b= const c=const a= −b lim_(x→1) ((ax −a)/( (√(1+3x)) −2)) =c lim_(x→0) ((a(x−1)∙((√(1+3x)) +2))/(3(x−1)))= c 4a=3c= −4b 2a − 2b +3c = 2a+2a+3c=4a+3c=6c 2a−2b+3c= 6c=8a= −8b

$$\boldsymbol{\mathrm{lim}}_{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{1}} \frac{\boldsymbol{\mathrm{ax}}+\boldsymbol{\mathrm{b}}}{\:\sqrt{\mathrm{1}+\mathrm{3}\boldsymbol{\mathrm{x}}}\:−\mathrm{2}}\:=\:\boldsymbol{\mathrm{c}} \\ $$$$\:\:\boldsymbol{\mathrm{a}}=\boldsymbol{\mathrm{const}}\:\:\:\:\:\boldsymbol{\mathrm{b}}=\:\boldsymbol{\mathrm{const}}\:\:\:\:\:\boldsymbol{\mathrm{c}}=\boldsymbol{\mathrm{const}} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{a}}=\:−\boldsymbol{\mathrm{b}} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{lim}}_{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{1}} \:\frac{\boldsymbol{\mathrm{ax}}\:−\boldsymbol{\mathrm{a}}}{\:\sqrt{\mathrm{1}+\mathrm{3}\boldsymbol{\mathrm{x}}}\:−\mathrm{2}}\:=\boldsymbol{\mathrm{c}} \\ $$$$\:\:\:\boldsymbol{\mathrm{lim}}_{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} \:\frac{\boldsymbol{\mathrm{a}}\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\centerdot\left(\sqrt{\mathrm{1}+\mathrm{3}\boldsymbol{\mathrm{x}}}\:+\mathrm{2}\right)}{\mathrm{3}\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)}=\:\boldsymbol{\mathrm{c}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{4}\boldsymbol{\mathrm{a}}=\mathrm{3}\boldsymbol{\mathrm{c}}=\:−\mathrm{4}\boldsymbol{\mathrm{b}} \\ $$$$\:\mathrm{2}\boldsymbol{\mathrm{a}}\:−\:\mathrm{2}\boldsymbol{\mathrm{b}}\:+\mathrm{3}\boldsymbol{\mathrm{c}}\:=\:\mathrm{2}\boldsymbol{\mathrm{a}}+\mathrm{2}\boldsymbol{\mathrm{a}}+\mathrm{3}\boldsymbol{\mathrm{c}}=\mathrm{4}\boldsymbol{\mathrm{a}}+\mathrm{3}\boldsymbol{\mathrm{c}}=\mathrm{6}\boldsymbol{\mathrm{c}} \\ $$$$\mathrm{2}\boldsymbol{\mathrm{a}}−\mathrm{2}\boldsymbol{\mathrm{b}}+\mathrm{3}\boldsymbol{\mathrm{c}}=\:\mathrm{6}\boldsymbol{\mathrm{c}}=\mathrm{8}\boldsymbol{\mathrm{a}}=\:−\mathrm{8}\boldsymbol{\mathrm{b}} \\ $$$$ \\ $$

Answered by a.lgnaoui last updated on 12/Jan/23

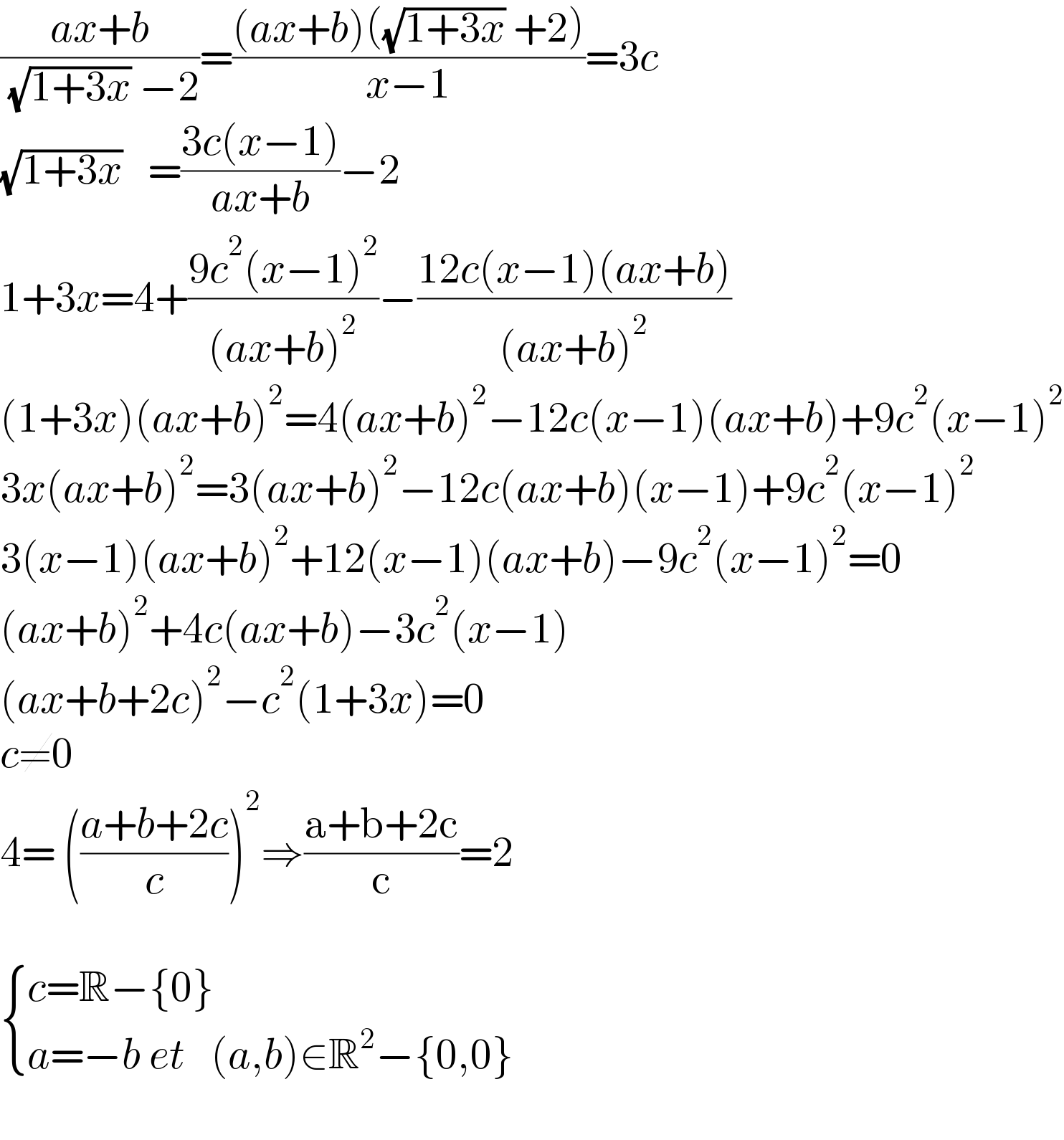
((ax+b)/( (√(1+3x)) −2))=(((ax+b)((√(1+3x)) +2))/(x−1))=3c (√(1+3x)) =((3c(x−1))/(ax+b))−2 1+3x=4+((9c^2 (x−1)^2 )/((ax+b)^2 ))−((12c(x−1)(ax+b))/((ax+b)^2 )) (1+3x)(ax+b)^2 =4(ax+b)^2 −12c(x−1)(ax+b)+9c^2 (x−1)^2 3x(ax+b)^2 =3(ax+b)^2 −12c(ax+b)(x−1)+9c^2 (x−1)^2 3(x−1)(ax+b)^2 +12(x−1)(ax+b)−9c^2 (x−1)^2 =0 (ax+b)^2 +4c(ax+b)−3c^2 (x−1) (ax+b+2c)^2 −c^2 (1+3x)=0 c≠0 4= (((a+b+2c)/c))^2 ⇒((a+b+2c)/c)=2 { ((c=R−{0})),((a=−b et (a,b)∈R^2 −{0,0})) :}

$$\frac{{ax}+{b}}{\:\sqrt{\mathrm{1}+\mathrm{3}{x}}\:−\mathrm{2}}=\frac{\left({ax}+{b}\right)\left(\sqrt{\mathrm{1}+\mathrm{3}{x}}\:+\mathrm{2}\right)}{{x}−\mathrm{1}}=\mathrm{3}{c} \\ $$$$\sqrt{\mathrm{1}+\mathrm{3}{x}}\:\:\:=\frac{\mathrm{3}{c}\left({x}−\mathrm{1}\right)}{{ax}+{b}}−\mathrm{2} \\ $$$$\mathrm{1}+\mathrm{3}{x}=\mathrm{4}+\frac{\mathrm{9}{c}^{\mathrm{2}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} }{\left({ax}+{b}\right)^{\mathrm{2}} }−\frac{\mathrm{12}{c}\left({x}−\mathrm{1}\right)\left({ax}+{b}\right)}{\left({ax}+{b}\right)^{\mathrm{2}} } \\ $$$$\left(\mathrm{1}+\mathrm{3}{x}\right)\left({ax}+{b}\right)^{\mathrm{2}} =\mathrm{4}\left({ax}+{b}\right)^{\mathrm{2}} −\mathrm{12}{c}\left({x}−\mathrm{1}\right)\left({ax}+{b}\right)+\mathrm{9}{c}^{\mathrm{2}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{3}{x}\left({ax}+{b}\right)^{\mathrm{2}} =\mathrm{3}\left({ax}+{b}\right)^{\mathrm{2}} −\mathrm{12}{c}\left({ax}+{b}\right)\left({x}−\mathrm{1}\right)+\mathrm{9}{c}^{\mathrm{2}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{3}\left({x}−\mathrm{1}\right)\left({ax}+{b}\right)^{\mathrm{2}} +\mathrm{12}\left({x}−\mathrm{1}\right)\left({ax}+{b}\right)−\mathrm{9}{c}^{\mathrm{2}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({ax}+{b}\right)^{\mathrm{2}} +\mathrm{4}{c}\left({ax}+{b}\right)−\mathrm{3}{c}^{\mathrm{2}} \left({x}−\mathrm{1}\right) \\ $$$$\left({ax}+{b}+\mathrm{2}{c}\right)^{\mathrm{2}} −{c}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3}{x}\right)=\mathrm{0} \\ $$$${c}\neq\mathrm{0} \\ $$$$\mathrm{4}=\:\left(\frac{{a}+{b}+\mathrm{2}{c}}{{c}}\right)^{\mathrm{2}} \Rightarrow\frac{\mathrm{a}+\mathrm{b}+\mathrm{2c}}{\mathrm{c}}=\mathrm{2} \\ $$$$ \\ $$$$\begin{cases}{{c}=\mathbb{R}−\left\{\mathrm{0}\right\}}\\{{a}=−{b}\:{et}\:\:\:\left({a},{b}\right)\in\mathbb{R}^{\mathrm{2}} −\left\{\mathrm{0},\mathrm{0}\right\}}\end{cases} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com