Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 188933 by horsebrand11 last updated on 09/Mar/23

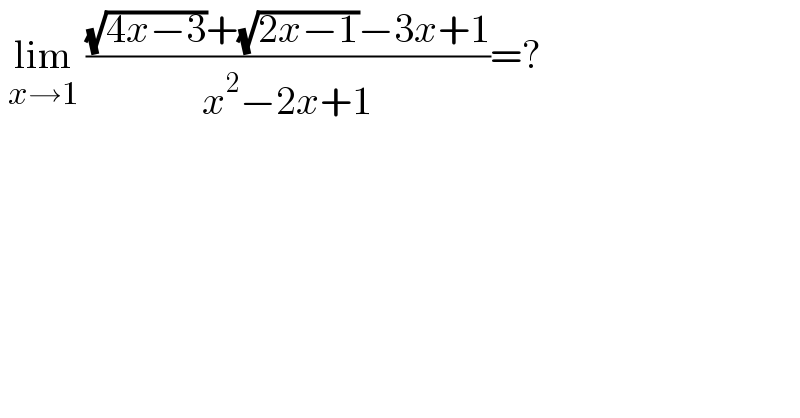
lim_(x→1) (((√(4x−3))+(√(2x−1))−3x+1)/(x^2 −2x+1))=?

$$\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{4}{x}−\mathrm{3}}+\sqrt{\mathrm{2}{x}−\mathrm{1}}−\mathrm{3}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}=? \\ $$

Commented by TUN last updated on 09/Mar/23

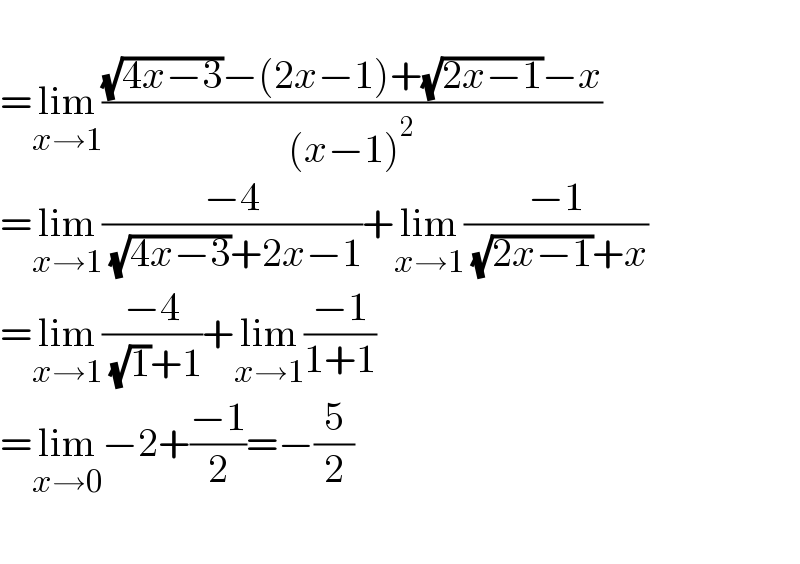
=lim_(x→1) (((√(4x−3))−(2x−1)+(√(2x−1))−x)/((x−1)^2 )) =lim_(x→1) ((−4)/( (√(4x−3))+2x−1))+lim_(x→1) ((−1)/( (√(2x−1))+x)) =lim_(x→1) ((−4)/( (√1)+1))+lim_(x→1) ((−1)/(1+1)) =lim_(x→0) −2+((−1)/2)=−(5/2)

$$ \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\sqrt{\mathrm{4}{x}−\mathrm{3}}−\left(\mathrm{2}{x}−\mathrm{1}\right)+\sqrt{\mathrm{2}{x}−\mathrm{1}}−{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{−\mathrm{4}}{\:\sqrt{\mathrm{4}{x}−\mathrm{3}}+\mathrm{2}{x}−\mathrm{1}}+\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}{x}−\mathrm{1}}+{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{−\mathrm{4}}{\:\sqrt{\mathrm{1}}+\mathrm{1}}+\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{−\mathrm{1}}{\mathrm{1}+\mathrm{1}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−\mathrm{2}+\frac{−\mathrm{1}}{\mathrm{2}}=−\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$ \\ $$

Answered by floor(10²Eta[1]) last updated on 09/Mar/23

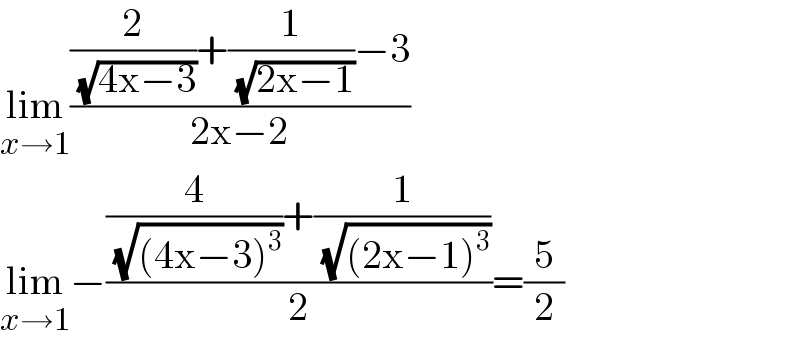
lim_(x→1) (((2/( (√(4x−3))))+(1/( (√(2x−1))))−3)/(2x−2)) lim_(x→1) −(((4/( (√((4x−3)^3 ))))+(1/( (√((2x−1)^3 )))))/2)=(5/2)

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\frac{\mathrm{2}}{\:\sqrt{\mathrm{4x}−\mathrm{3}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2x}−\mathrm{1}}}−\mathrm{3}}{\mathrm{2x}−\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}−\frac{\frac{\mathrm{4}}{\:\sqrt{\left(\mathrm{4x}−\mathrm{3}\right)^{\mathrm{3}} }}+\frac{\mathrm{1}}{\:\sqrt{\left(\mathrm{2x}−\mathrm{1}\right)^{\mathrm{3}} }}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$

Answered by cortano12 last updated on 09/Mar/23

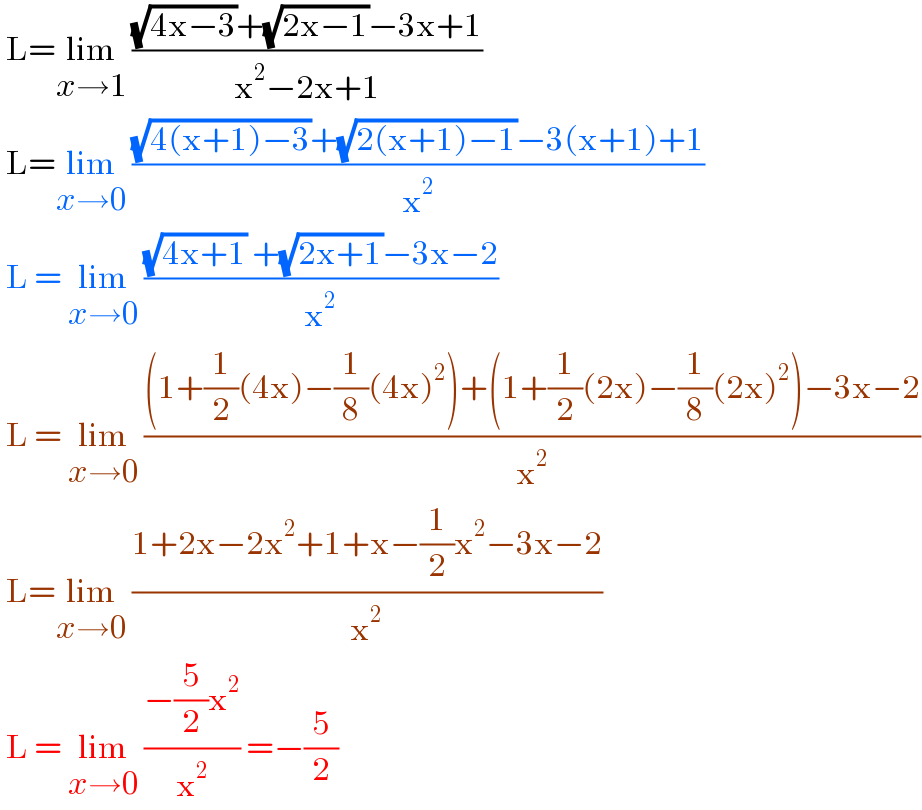
L=lim_(x→1) (((√(4x−3))+(√(2x−1))−3x+1)/(x^2 −2x+1)) L=lim_(x→0) (((√(4(x+1)−3))+(√(2(x+1)−1))−3(x+1)+1)/x^2 ) L = lim_(x→0) (((√(4x+1)) +(√(2x+1))−3x−2)/x^2 ) L = lim_(x→0) (((1+(1/2)(4x)−(1/8)(4x)^2 )+(1+(1/2)(2x)−(1/8)(2x)^2 )−3x−2)/x^2 ) L=lim_(x→0) ((1+2x−2x^2 +1+x−(1/2)x^2 −3x−2)/x^2 ) L = lim_(x→0) ((−(5/2)x^2 )/x^2 ) =−(5/2)

$$\:\mathrm{L}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{4x}−\mathrm{3}}+\sqrt{\mathrm{2x}−\mathrm{1}}−\mathrm{3x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}} \\ $$$$\:\mathrm{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{4}\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{3}}+\sqrt{\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{1}}−\mathrm{3}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\mathrm{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{4x}+\mathrm{1}}\:+\sqrt{\mathrm{2x}+\mathrm{1}}−\mathrm{3x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\mathrm{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4x}\right)−\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{4x}\right)^{\mathrm{2}} \right)+\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2x}\right)−\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{2x}\right)^{\mathrm{2}} \right)−\mathrm{3x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\mathrm{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}+\mathrm{2x}−\mathrm{2x}^{\mathrm{2}} +\mathrm{1}+\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\mathrm{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\frac{\mathrm{5}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\:=−\frac{\mathrm{5}}{\mathrm{2}}\: \\ $$

Commented by leandrosriv02 last updated on 11/Mar/23

L=lim_(x→1) (((√(4x−3))+(√(2x−1))−3x+1)/(x^2 −2x+1)) L=lim_(x→0) (((√(4(x+1)−3))+(√(2(x+1)−1))−3(x+1)+1)/x^2 ) L = lim_(x→0) (((√(4x+1)) +(√(2x+1))−3x−2)/x^2 ) L = lim_(x→0) (((1+(1/2)(4x)−(1/8)(4x)^2 )+(1+(1/2)(2x)−(1/8)(2x)^2 )−3x−2)/x^2 ) L=lim_(x→0) ((1+2x−2x^2 +1+x−(1/2)x^2 −3x−2)/x^2 ) L = lim_(x→0) ((−(5/2)x^2 )/x^2 ) =−(5/2) lim_(x→1) (((√(4x−3))+(√(2x−1))−3x+1)/(x^2 −2x+1))=−(5/2) determinant ((x,(1.1),(1.01),(1.001),(0.999),(0.99),(0.9)),((f(x)),(−2.1),(−2.45),(−2.495),(−2.504),(−2.54),(−3.0))) lim_(x→1^− ) f(x)=−(5/2) lim_(x→1^+ ) f(x)=−(5/2) El limite existe y es discontinua evitable en x=1

$$ \\ $$$$\:\mathrm{L}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{4x}−\mathrm{3}}+\sqrt{\mathrm{2x}−\mathrm{1}}−\mathrm{3x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}} \\ $$$$\:\mathrm{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{4}\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{3}}+\sqrt{\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{1}}−\mathrm{3}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\mathrm{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{4x}+\mathrm{1}}\:+\sqrt{\mathrm{2x}+\mathrm{1}}−\mathrm{3x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\mathrm{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4x}\right)−\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{4x}\right)^{\mathrm{2}} \right)+\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2x}\right)−\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{2x}\right)^{\mathrm{2}} \right)−\mathrm{3x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\mathrm{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}+\mathrm{2x}−\mathrm{2x}^{\mathrm{2}} +\mathrm{1}+\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\mathrm{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\frac{\mathrm{5}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\:=−\frac{\mathrm{5}}{\mathrm{2}}\: \\ $$$$ \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{4x}−\mathrm{3}}+\sqrt{\mathrm{2x}−\mathrm{1}}−\mathrm{3x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}}=−\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\begin{array}{|c|c|}{{x}}&\hline{\mathrm{1}.\mathrm{1}}&\hline{\mathrm{1}.\mathrm{01}}&\hline{\mathrm{1}.\mathrm{001}}&\hline{\mathrm{0}.\mathrm{999}}&\hline{\mathrm{0}.\mathrm{99}}&\hline{\mathrm{0}.\mathrm{9}}\\{{f}\left({x}\right)}&\hline{−\mathrm{2}.\mathrm{1}}&\hline{−\mathrm{2}.\mathrm{45}}&\hline{−\mathrm{2}.\mathrm{495}}&\hline{−\mathrm{2}.\mathrm{504}}&\hline{−\mathrm{2}.\mathrm{54}}&\hline{−\mathrm{3}.\mathrm{0}}\\\hline\end{array} \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}{f}\left({x}\right)=−\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}{f}\left({x}\right)=−\frac{\mathrm{5}}{\mathrm{2}} \\ $$$${El}\:{limite}\:{existe}\:{y}\:{es}\:{discontinua}\:{evitable}\:{en}\:{x}=\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com