
Question Number 154776 by john_santu last updated on 21/Sep/21
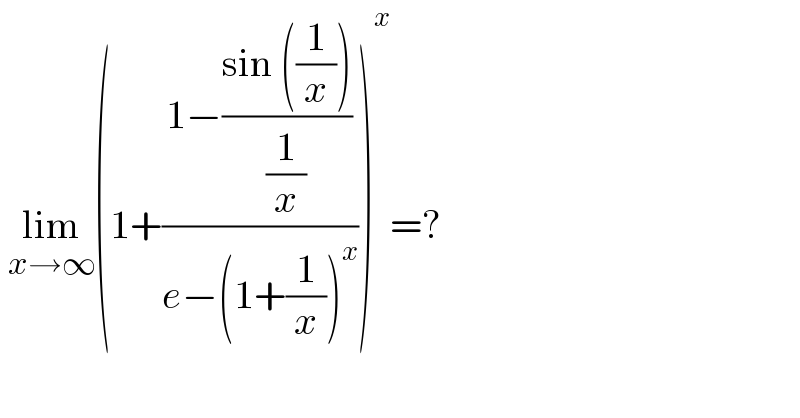
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}−\frac{\mathrm{sin}\:\left(\frac{\mathrm{1}}{{x}}\right)}{\frac{\mathrm{1}}{{x}}}}{{e}−\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} }\right)^{{x}} =? \\ $$
Commented by mathdanisur last updated on 21/Sep/21
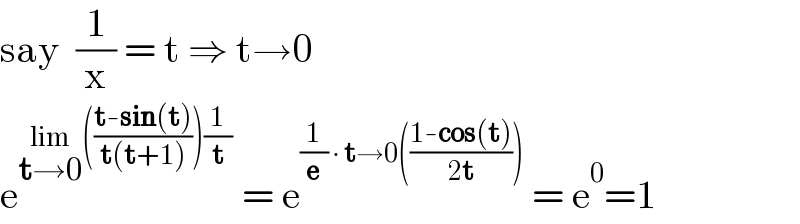
$$\mathrm{say}\:\:\frac{\mathrm{1}}{\mathrm{x}}\:=\:\mathrm{t}\:\Rightarrow\:\mathrm{t}\rightarrow\mathrm{0} \\ $$$$\mathrm{e}^{\underset{\boldsymbol{\mathrm{t}}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\boldsymbol{\mathrm{t}}-\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)}{\boldsymbol{\mathrm{t}}\left(\boldsymbol{\mathrm{t}}+\mathrm{1}\right)}\right)\frac{\mathrm{1}}{\boldsymbol{\mathrm{t}}}} \:=\:\mathrm{e}^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{e}}}\:\centerdot\:\boldsymbol{\mathrm{t}}\rightarrow\mathrm{0}\left(\frac{\mathrm{1}-\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{t}}\right)}{\mathrm{2}\boldsymbol{\mathrm{t}}}\right)} \:=\:\mathrm{e}^{\mathrm{0}} =\mathrm{1} \\ $$
