
Question Number 109733 by bobhans last updated on 25/Aug/20
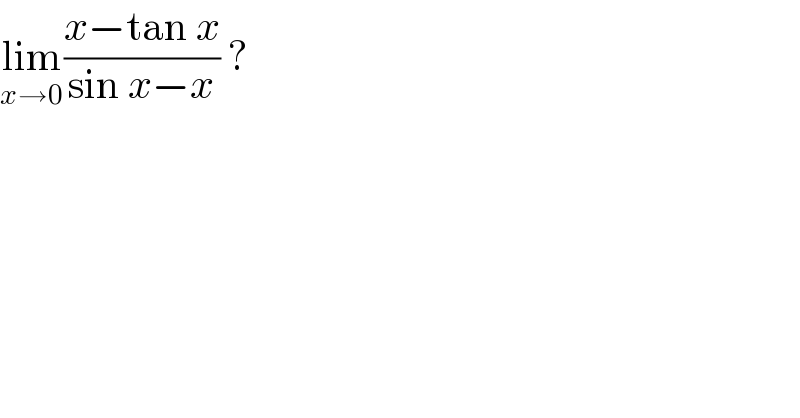
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−\mathrm{tan}\:{x}}{\mathrm{sin}\:{x}−{x}}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 25/Aug/20

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}}{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}−{x}}=\mathrm{2} \\ $$
Answered by 1549442205PVT last updated on 25/Aug/20
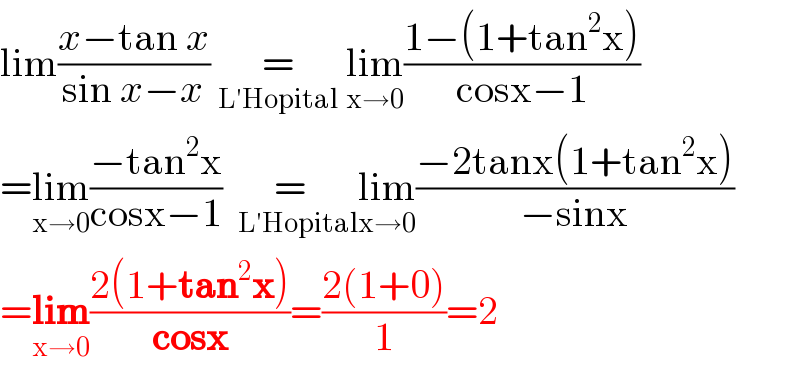
$$\mathrm{lim}\frac{{x}−\mathrm{tan}\:{x}}{\mathrm{sin}\:{x}−{x}}\:\underset{\mathrm{L}'\mathrm{Hopital}} {\:\:\:=\:\:\:}\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{cosx}−\mathrm{1}} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\mathrm{cosx}−\mathrm{1}}\:\:\underset{\mathrm{L}'\mathrm{Hopital}} {\:=\:\:\:}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2tanx}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)}{−\mathrm{sinx}} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\boldsymbol{\mathrm{lim}}}\frac{\mathrm{2}\left(\mathrm{1}+\boldsymbol{\mathrm{tan}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{cosx}}}=\frac{\mathrm{2}\left(\mathrm{1}+\mathrm{0}\right)}{\mathrm{1}}=\mathrm{2}\: \\ $$
