
Question Number 114405 by bemath last updated on 19/Sep/20
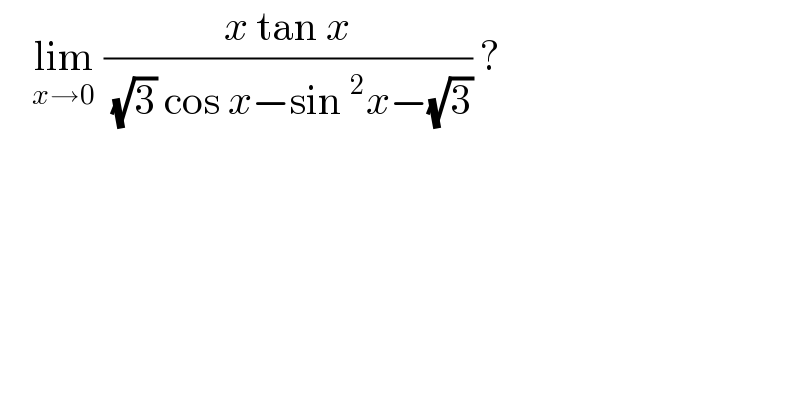
$$\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\:\mathrm{tan}\:{x}}{\:\sqrt{\mathrm{3}}\:\mathrm{cos}\:{x}−\mathrm{sin}\:^{\mathrm{2}} {x}−\sqrt{\mathrm{3}}}\:? \\ $$
Answered by bobhans last updated on 19/Sep/20
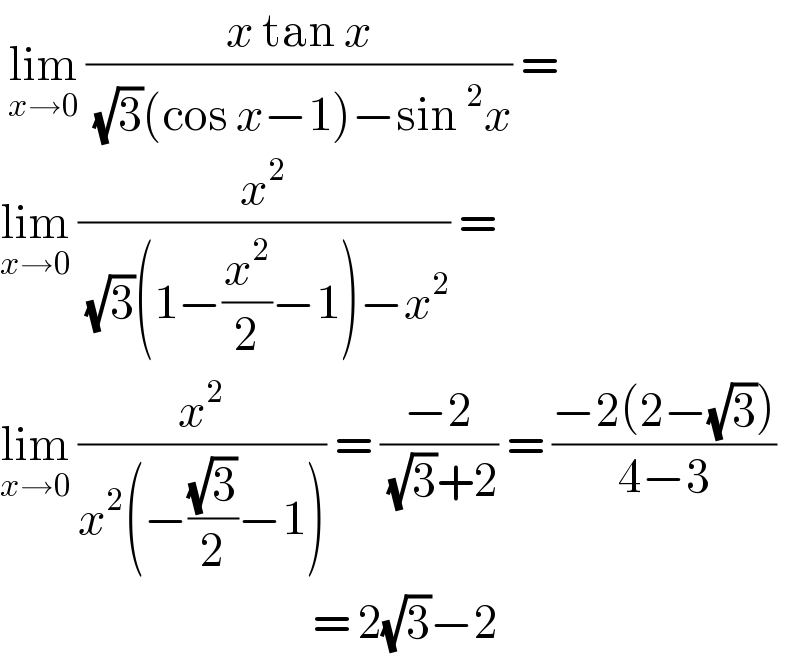
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\:\mathrm{tan}\:{x}}{\:\sqrt{\mathrm{3}}\left(\mathrm{cos}\:{x}−\mathrm{1}\right)−\mathrm{sin}\:^{\mathrm{2}} {x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{3}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}\right)−{x}^{\mathrm{2}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \left(−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{1}\right)}\:=\:\frac{−\mathrm{2}}{\:\sqrt{\mathrm{3}}+\mathrm{2}}\:=\:\frac{−\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}{\mathrm{4}−\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2} \\ $$
Commented by bemath last updated on 19/Sep/20

$${gave}\:{kudos}\:\checkmark\Bumpeq \\ $$
Answered by Dwaipayan Shikari last updated on 19/Sep/20
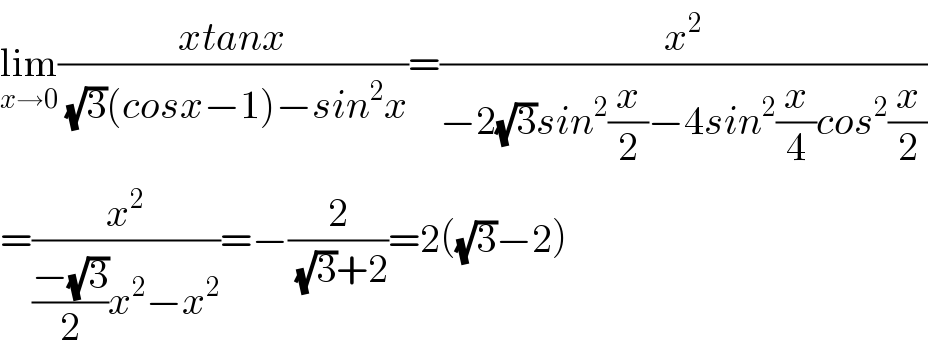
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{xtanx}}{\:\sqrt{\mathrm{3}}\left({cosx}−\mathrm{1}\right)−{sin}^{\mathrm{2}} {x}}=\frac{{x}^{\mathrm{2}} }{−\mathrm{2}\sqrt{\mathrm{3}}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{4}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{4}}{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$$$=\frac{{x}^{\mathrm{2}} }{\frac{−\sqrt{\mathrm{3}}}{\mathrm{2}}{x}^{\mathrm{2}} −{x}^{\mathrm{2}} }=−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}+\mathrm{2}}=\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{2}\right) \\ $$
