Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 203247 by mathlove last updated on 13/Jan/24

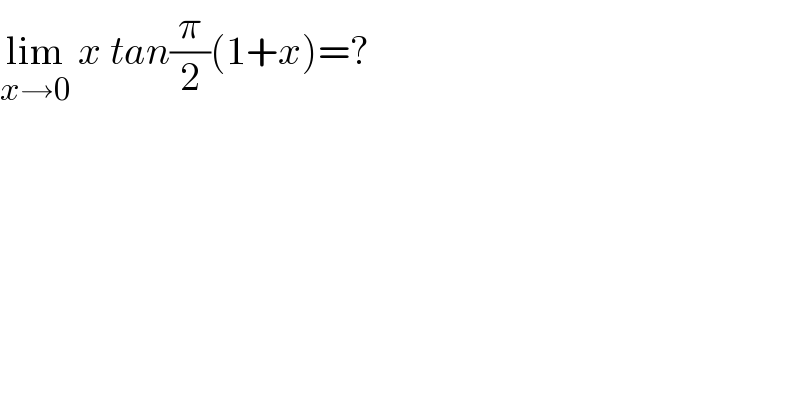
lim_(x→0) x tan(π/2)(1+x)=?

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}\:{tan}\frac{\pi}{\mathrm{2}}\left(\mathrm{1}+{x}\right)=? \\ $$

Answered by MM42 last updated on 13/Jan/24

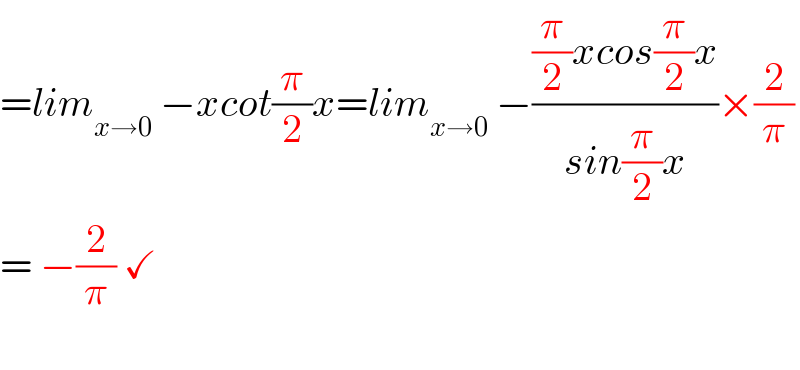
=lim_(x→0) −xcot(π/2)x=lim_(x→0) −(((π/2)xcos(π/2)x)/(sin(π/2)x))×(2/π) = −(2/π) ✓

$$={lim}_{{x}\rightarrow\mathrm{0}} \:−{xcot}\frac{\pi}{\mathrm{2}}{x}={lim}_{{x}\rightarrow\mathrm{0}} \:−\frac{\frac{\pi}{\mathrm{2}}{xcos}\frac{\pi}{\mathrm{2}}{x}}{{sin}\frac{\pi}{\mathrm{2}}{x}}×\frac{\mathrm{2}}{\pi} \\ $$$$=\:−\frac{\mathrm{2}}{\pi}\:\checkmark \\ $$$$ \\ $$

Commented by mathlove last updated on 13/Jan/24

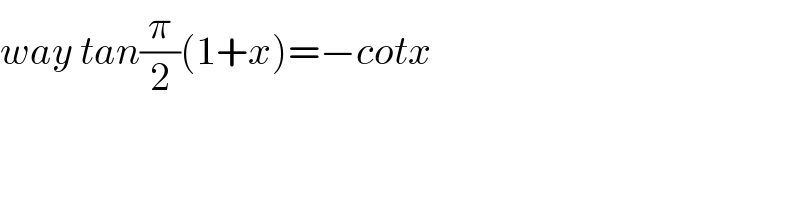
way tan(π/2)(1+x)=−cotx

$${way}\:{tan}\frac{\pi}{\mathrm{2}}\left(\mathrm{1}+{x}\right)=−{cotx} \\ $$

Commented by MM42 last updated on 13/Jan/24

ok −cot(π/2)x

$${ok} \\ $$$$−{cot}\frac{\pi}{\mathrm{2}}{x} \\ $$

Answered by mr W last updated on 13/Jan/24

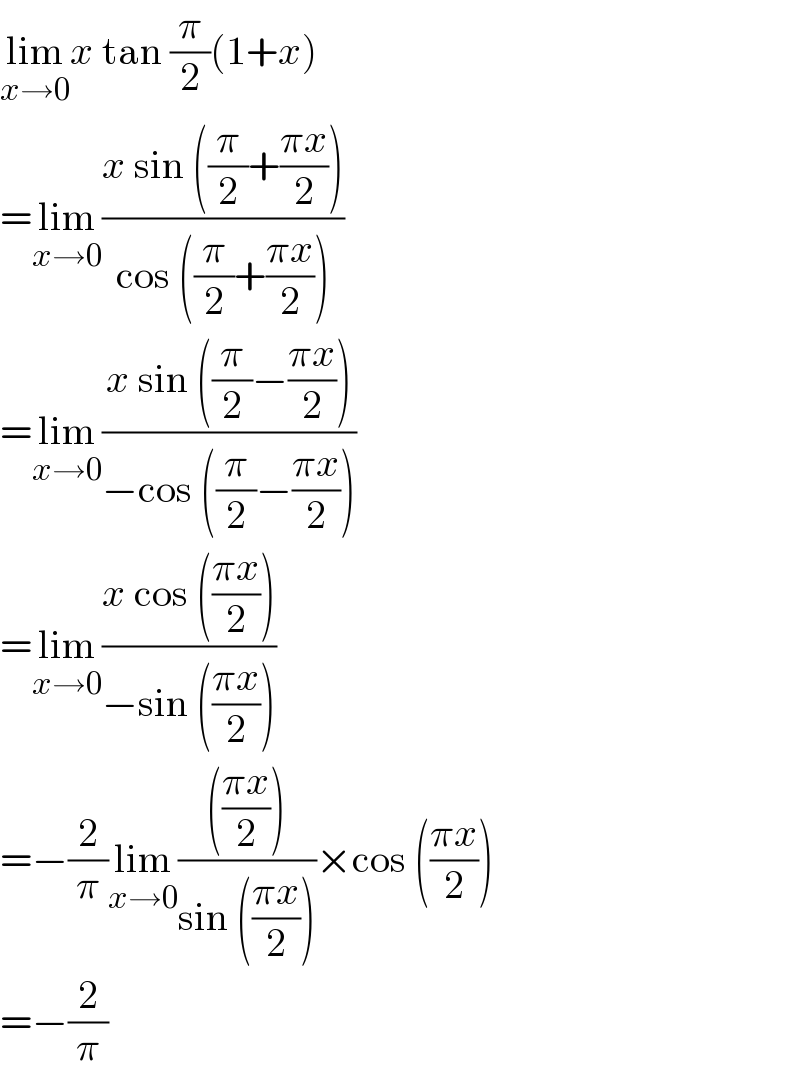
lim_(x→0) x tan (π/2)(1+x) =lim_(x→0) ((x sin ((π/2)+((πx)/2)))/(cos ((π/2)+((πx)/2)))) =lim_(x→0) ((x sin ((π/2)−((πx)/2)))/(−cos ((π/2)−((πx)/2)))) =lim_(x→0) ((x cos (((πx)/2)))/(−sin (((πx)/2)))) =−(2/π)lim_(x→0) (((((πx)/2)))/(sin (((πx)/2))))×cos (((πx)/2)) =−(2/π)

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{x}\:\mathrm{tan}\:\frac{\pi}{\mathrm{2}}\left(\mathrm{1}+{x}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}+\frac{\pi{x}}{\mathrm{2}}\right)}{\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}+\frac{\pi{x}}{\mathrm{2}}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\pi{x}}{\mathrm{2}}\right)}{−\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\pi{x}}{\mathrm{2}}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}\:\mathrm{cos}\:\left(\frac{\pi{x}}{\mathrm{2}}\right)}{−\mathrm{sin}\:\left(\frac{\pi{x}}{\mathrm{2}}\right)} \\ $$$$=−\frac{\mathrm{2}}{\pi}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\pi{x}}{\mathrm{2}}\right)}{\mathrm{sin}\:\left(\frac{\pi{x}}{\mathrm{2}}\right)}×\mathrm{cos}\:\left(\frac{\pi{x}}{\mathrm{2}}\right) \\ $$$$=−\frac{\mathrm{2}}{\pi} \\ $$

Commented by mathlove last updated on 13/Jan/24

thats right thanks sir

$${thats}\:{right} \\ $$$${thanks}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com