
Question Number 170182 by mathlove last updated on 18/May/22
![lim_(x→0) [x∙sin(1/x)]=?](Q170182.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[{x}\centerdot{sin}\frac{\mathrm{1}}{{x}}\right]=? \\ $$
Commented by mr W last updated on 18/May/22
![has [ ] special meaning? or you just mean lim_(x→0) (x∙sin(1/x))=?](Q170192.png)
$${has}\:\left[\:\:\right]\:{special}\:{meaning}?\:{or}\:{you}\:{just}\:{mean} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left({x}\centerdot{sin}\frac{\mathrm{1}}{{x}}\right)=? \\ $$
Answered by mr W last updated on 18/May/22
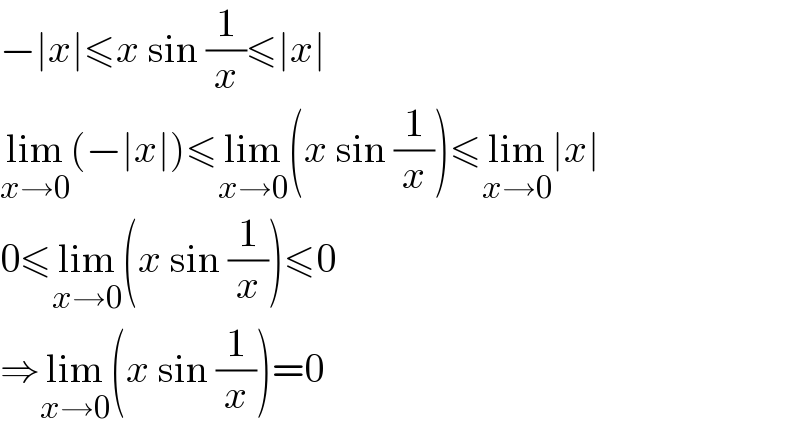
$$−\mid{x}\mid\leqslant{x}\:\mathrm{sin}\:\frac{\mathrm{1}}{{x}}\leqslant\mid{x}\mid \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−\mid{x}\mid\right)\leqslant\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({x}\:\mathrm{sin}\:\frac{\mathrm{1}}{{x}}\right)\leqslant\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\mid{x}\mid \\ $$$$\mathrm{0}\leqslant\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({x}\:\mathrm{sin}\:\frac{\mathrm{1}}{{x}}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({x}\:\mathrm{sin}\:\frac{\mathrm{1}}{{x}}\right)=\mathrm{0} \\ $$
Commented by mathlove last updated on 18/May/22

$${thanks} \\ $$
