
Question Number 129584 by bemath last updated on 16/Jan/21
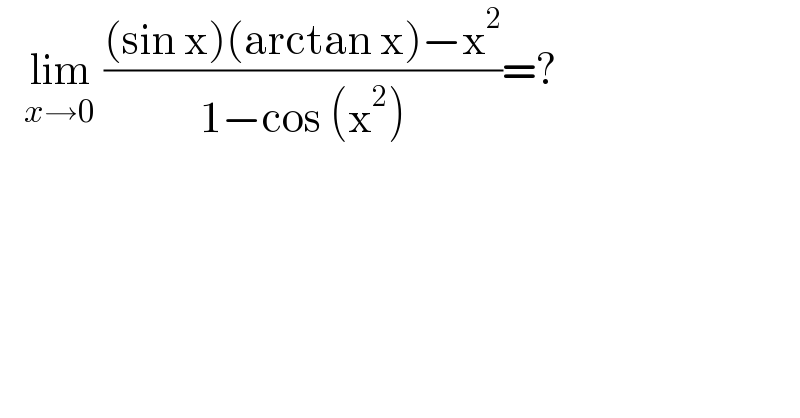
$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{sin}\:\mathrm{x}\right)\left(\mathrm{arctan}\:\mathrm{x}\right)−\mathrm{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{cos}\:\left(\mathrm{x}^{\mathrm{2}} \right)}=? \\ $$
Answered by liberty last updated on 16/Jan/21
![lim_(x→0) (((x−(x^3 /6)+(x^5 /(120)))(x−(x^3 /3)+(x^5 /5))−x^2 )/(1−(1−(x^4 /2)))) = lim_(x→0) ((x^2 [(1−(x^2 /6)+(x^4 /(120)))(1−(x^2 /3)+(x^4 /5))−1 ])/(x^4 /2)) lim_(x→0) ((2(1−((x^2 /3)−(x^4 /5))−(x^2 /6)(1−(x^2 /3)+(x^4 /5))+(x^4 /(120))(1−(x^3 /3)+(x^4 /5))−1))/x^2 )= = 2(−(1/3)−(1/6))=2(−(1/2))=−1](Q129585.png)
$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}+\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{120}}\right)\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{5}}\right)−\mathrm{x}^{\mathrm{2}} }{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{2}}\right)}\:= \\ $$$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{2}} \:\left[\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{120}}\right)\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{5}}\right)−\mathrm{1}\:\right]}{\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{2}}} \\ $$$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left(\mathrm{1}−\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{5}}\right)−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{5}}\right)+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{120}}\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{5}}\right)−\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}} }= \\ $$$$\:=\:\mathrm{2}\left(−\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{6}}\right)=\mathrm{2}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)=−\mathrm{1} \\ $$
