Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 187092 by cortano12 last updated on 13/Feb/23

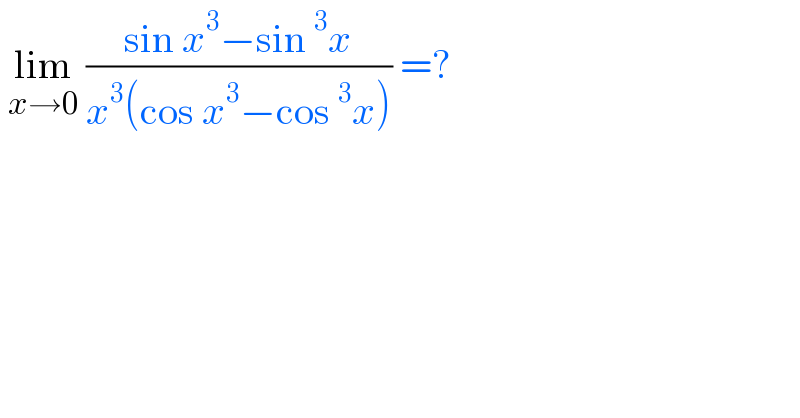
lim_(x→0) ((sin x^3 −sin^3 x)/(x^3 (cos x^3 −cos^3 x))) =?

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}^{\mathrm{3}} −\mathrm{sin}\:^{\mathrm{3}} {x}}{{x}^{\mathrm{3}} \left(\mathrm{cos}\:{x}^{\mathrm{3}} −\mathrm{cos}\:^{\mathrm{3}} {x}\right)}\:=? \\ $$

Answered by Farhadazizi last updated on 13/Feb/23

=(0/0)→Hop→ =lim_(x→0 ) ((3x^2 cosx^3 −3sinxcos^2 x)/(3x^2 (cosx^3 −cos^3 x)+x^3 (−3x^2 sinx^3 +3cosxsin^2 x)))=(0/0)→Hop→ =lim_(x→0) ((3[(2xcosx^3 −3x^4 sinx^3 )−(cos^3 x+sinxsin2x)])/(3[2x(cosx^3 −cos^3 x)+x^2 (−3x^2 sinx^3 +3cosxsin^2 x)+3x^2 (−x^2 sinx^3 +cosxsin^2 x)+x^3 (−2xsinx^3 −3x^4 cosx^3 −sin^3 x+2sinxcos^2 x)))=((−1)/0)???

$$=\frac{\mathrm{0}}{\mathrm{0}}\rightarrow{Hop}\rightarrow \\ $$$$=\underset{{x}\rightarrow\mathrm{0}\:\:} {\mathrm{lim}}\frac{\mathrm{3}{x}^{\mathrm{2}} {cosx}^{\mathrm{3}} −\mathrm{3}{sinxcos}^{\mathrm{2}} {x}}{\mathrm{3}{x}^{\mathrm{2}} \left({cosx}^{\mathrm{3}} −{cos}^{\mathrm{3}} {x}\right)+{x}^{\mathrm{3}} \left(−\mathrm{3}{x}^{\mathrm{2}} {sinx}^{\mathrm{3}} +\mathrm{3}{cosxsin}^{\mathrm{2}} {x}\right)}=\frac{\mathrm{0}}{\mathrm{0}}\rightarrow{Hop}\rightarrow \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}\left[\left(\mathrm{2}{xcosx}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{4}} {sinx}^{\mathrm{3}} \right)−\left({cos}^{\mathrm{3}} {x}+{sinxsin}\mathrm{2}{x}\right)\right]}{\mathrm{3}\left[\mathrm{2}{x}\left({cosx}^{\mathrm{3}} −{cos}^{\mathrm{3}} {x}\right)+{x}^{\mathrm{2}} \left(−\mathrm{3}{x}^{\mathrm{2}} {sinx}^{\mathrm{3}} +\mathrm{3}{cosxsin}^{\mathrm{2}} {x}\right)+\mathrm{3}{x}^{\mathrm{2}} \left(−{x}^{\mathrm{2}} {sinx}^{\mathrm{3}} +{cosxsin}^{\mathrm{2}} {x}\right)+{x}^{\mathrm{3}} \left(−\mathrm{2}{xsinx}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{4}} {cosx}^{\mathrm{3}} −{sin}^{\mathrm{3}} {x}+\mathrm{2}{sinxcos}^{\mathrm{2}} {x}\right)\right.}=\frac{−\mathrm{1}}{\mathrm{0}}??? \\ $$

Answered by ARUNG_Brandon_MBU last updated on 13/Feb/23

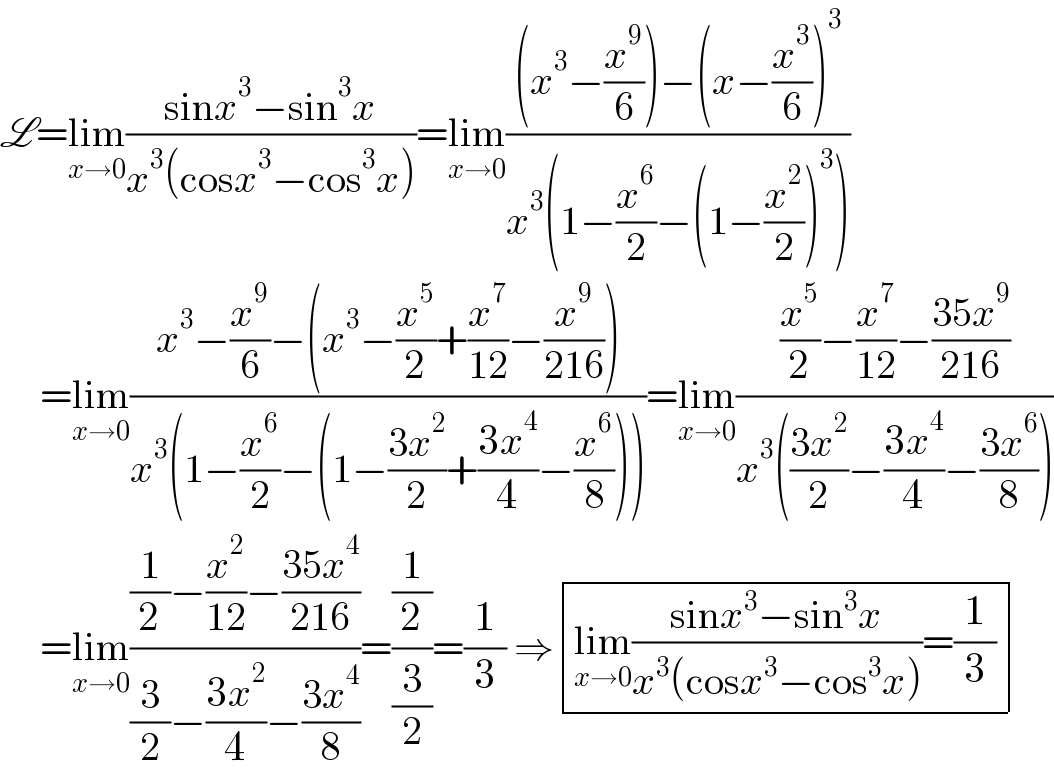
L=lim_(x→0) ((sinx^3 −sin^3 x)/(x^3 (cosx^3 −cos^3 x)))=lim_(x→0) (((x^3 −(x^9 /6))−(x−(x^3 /6))^3 )/(x^3 (1−(x^6 /2)−(1−(x^2 /2))^3 ))) =lim_(x→0) ((x^3 −(x^9 /6)−(x^3 −(x^5 /2)+(x^7 /(12))−(x^9 /(216))))/(x^3 (1−(x^6 /2)−(1−((3x^2 )/2)+((3x^4 )/4)−(x^6 /8)))))=lim_(x→0) (((x^5 /2)−(x^7 /(12))−((35x^9 )/(216)))/(x^3 (((3x^2 )/2)−((3x^4 )/4)−((3x^6 )/8)))) =lim_(x→0) (((1/2)−(x^2 /(12))−((35x^4 )/(216)))/((3/2)−((3x^2 )/4)−((3x^4 )/8)))=((1/2)/(3/2))=(1/3) ⇒ determinant (((lim_(x→0) ((sinx^3 −sin^3 x)/(x^3 (cosx^3 −cos^3 x)))=(1/3))))

$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}{x}^{\mathrm{3}} −\mathrm{sin}^{\mathrm{3}} {x}}{{x}^{\mathrm{3}} \left(\mathrm{cos}{x}^{\mathrm{3}} −\mathrm{cos}^{\mathrm{3}} {x}\right)}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({x}^{\mathrm{3}} −\frac{{x}^{\mathrm{9}} }{\mathrm{6}}\right)−\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)^{\mathrm{3}} }{{x}^{\mathrm{3}} \left(\mathrm{1}−\frac{{x}^{\mathrm{6}} }{\mathrm{2}}−\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{3}} \right)} \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{3}} −\frac{{x}^{\mathrm{9}} }{\mathrm{6}}−\left({x}^{\mathrm{3}} −\frac{{x}^{\mathrm{5}} }{\mathrm{2}}+\frac{{x}^{\mathrm{7}} }{\mathrm{12}}−\frac{{x}^{\mathrm{9}} }{\mathrm{216}}\right)}{{x}^{\mathrm{3}} \left(\mathrm{1}−\frac{{x}^{\mathrm{6}} }{\mathrm{2}}−\left(\mathrm{1}−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}{x}^{\mathrm{4}} }{\mathrm{4}}−\frac{{x}^{\mathrm{6}} }{\mathrm{8}}\right)\right)}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{x}^{\mathrm{5}} }{\mathrm{2}}−\frac{{x}^{\mathrm{7}} }{\mathrm{12}}−\frac{\mathrm{35}{x}^{\mathrm{9}} }{\mathrm{216}}}{{x}^{\mathrm{3}} \left(\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{3}{x}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{3}{x}^{\mathrm{6}} }{\mathrm{8}}\right)} \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}^{\mathrm{2}} }{\mathrm{12}}−\frac{\mathrm{35}{x}^{\mathrm{4}} }{\mathrm{216}}}{\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{3}{x}^{\mathrm{4}} }{\mathrm{8}}}=\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{3}}{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\begin{array}{|c|}{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}{x}^{\mathrm{3}} −\mathrm{sin}^{\mathrm{3}} {x}}{{x}^{\mathrm{3}} \left(\mathrm{cos}{x}^{\mathrm{3}} −\mathrm{cos}^{\mathrm{3}} {x}\right)}=\frac{\mathrm{1}}{\mathrm{3}}}\\\hline\end{array} \\ $$

Commented by cortano12 last updated on 14/Feb/23

yes...

$${yes}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com