
Question Number 62874 by solihin last updated on 26/Jun/19

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sin}\left(\mathrm{6}{x}\right)}{{tan}\left(\mathrm{5}{x}\right)} \\ $$$$ \\ $$$${how}\:\:{to}\:\:{solve}\:\:{this}\:\:{w}/{o}\:\:{L}'{hospital}'{s}\:\:{rule}? \\ $$
Commented by kaivan.ahmadi last updated on 26/Jun/19
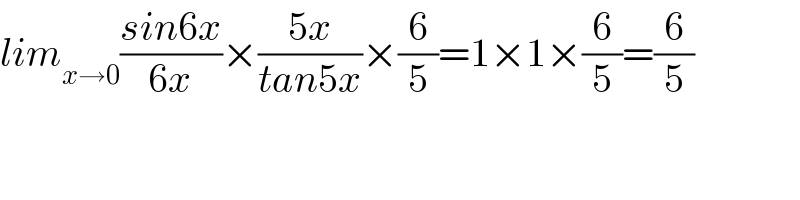
$${lim}_{{x}\rightarrow\mathrm{0}} \frac{{sin}\mathrm{6}{x}}{\mathrm{6}{x}}×\frac{\mathrm{5}{x}}{{tan}\mathrm{5}{x}}×\frac{\mathrm{6}}{\mathrm{5}}=\mathrm{1}×\mathrm{1}×\frac{\mathrm{6}}{\mathrm{5}}=\frac{\mathrm{6}}{\mathrm{5}} \\ $$
Commented by solihin last updated on 26/Jun/19

$${wow}\:\:{thx} \\ $$
Commented by mathmax by abdo last updated on 26/Jun/19
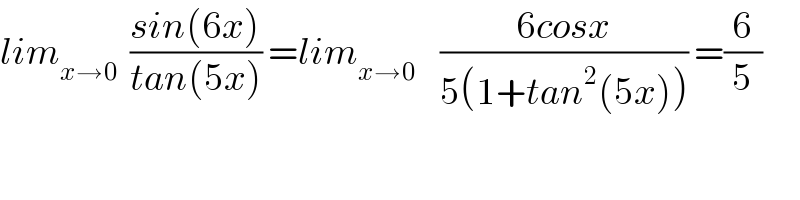
$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{sin}\left(\mathrm{6}{x}\right)}{{tan}\left(\mathrm{5}{x}\right)}\:={lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\frac{\mathrm{6}{cosx}}{\mathrm{5}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\mathrm{5}{x}\right)\right)}\:=\frac{\mathrm{6}}{\mathrm{5}} \\ $$
