
Question Number 122824 by bemath last updated on 19/Nov/20
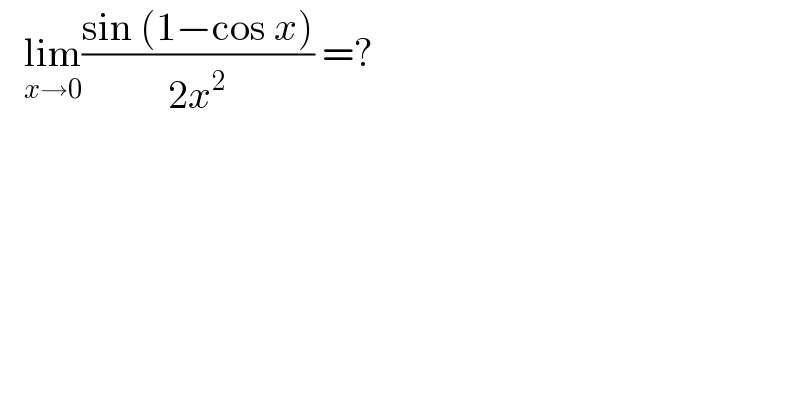
$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left(\mathrm{1}−\mathrm{cos}\:{x}\right)}{\mathrm{2}{x}^{\mathrm{2}} }\:=? \\ $$
Commented by bobhans last updated on 20/Nov/20
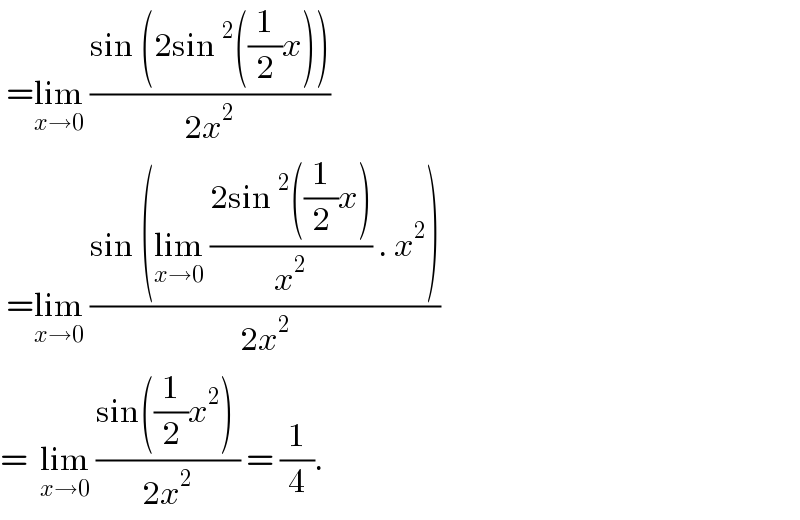
$$\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)\right)}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)}{{x}^{\mathrm{2}} }\:.\:{x}^{\mathrm{2}} \right)}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$=\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right)\:}{\mathrm{2}{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{4}}.\: \\ $$
Answered by liberty last updated on 19/Nov/20
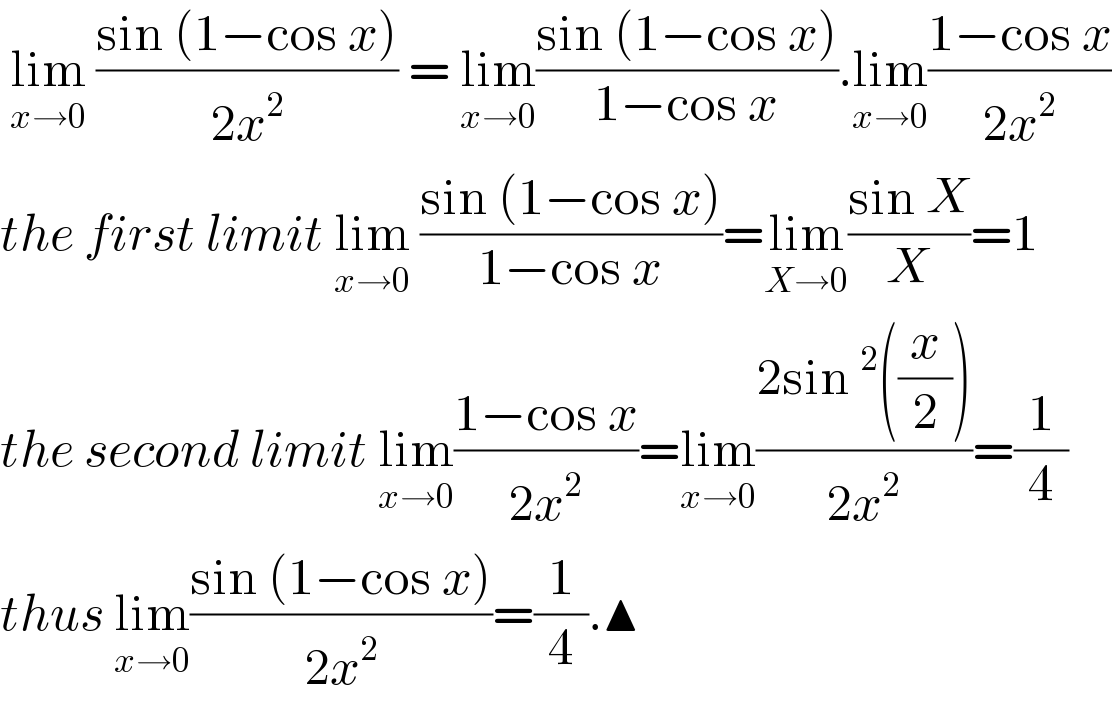
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{1}−\mathrm{cos}\:{x}\right)}{\mathrm{2}{x}^{\mathrm{2}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left(\mathrm{1}−\mathrm{cos}\:{x}\right)}{\mathrm{1}−\mathrm{cos}\:{x}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:{x}}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$${the}\:{first}\:{limit}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{1}−\mathrm{cos}\:{x}\right)}{\mathrm{1}−\mathrm{cos}\:{x}}=\underset{{X}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{X}}{{X}}=\mathrm{1} \\ $$$${the}\:{second}\:{limit}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:{x}}{\mathrm{2}{x}^{\mathrm{2}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${thus}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left(\mathrm{1}−\mathrm{cos}\:{x}\right)}{\mathrm{2}{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}.\blacktriangle \\ $$
Answered by mathmax by abdo last updated on 20/Nov/20
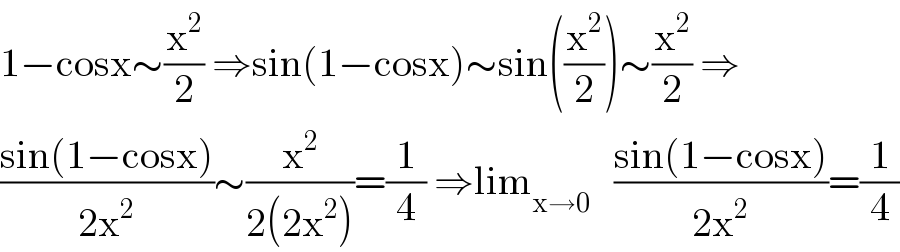
$$\mathrm{1}−\mathrm{cosx}\sim\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{sin}\left(\mathrm{1}−\mathrm{cosx}\right)\sim\mathrm{sin}\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)\sim\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{\mathrm{sin}\left(\mathrm{1}−\mathrm{cosx}\right)}{\mathrm{2x}^{\mathrm{2}} }\sim\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{2x}^{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{sin}\left(\mathrm{1}−\mathrm{cosx}\right)}{\mathrm{2x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
