
Question Number 175995 by sciencestudent last updated on 10/Sep/22
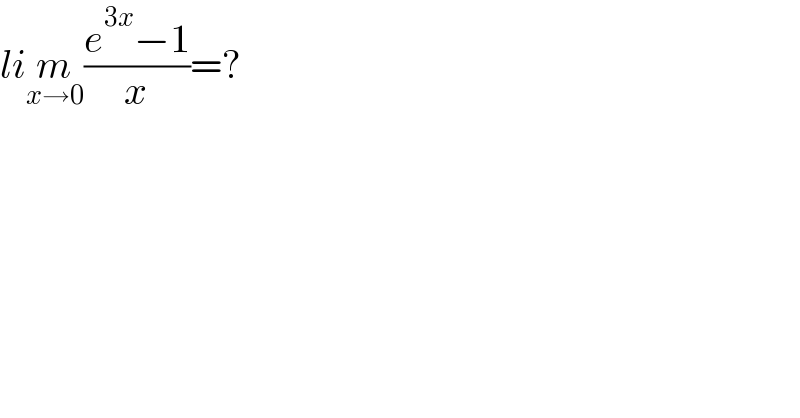
$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{{e}^{\mathrm{3}{x}} −\mathrm{1}}{{x}}=? \\ $$
Answered by Ar Brandon last updated on 10/Sep/22
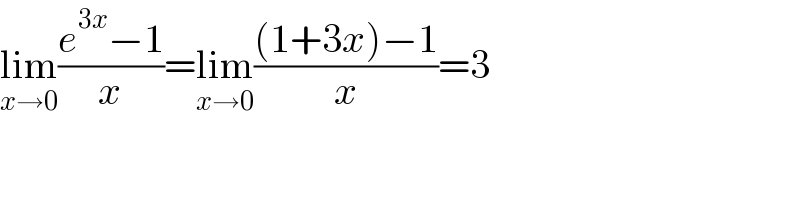
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\mathrm{3}{x}} −\mathrm{1}}{{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\mathrm{3}{x}\right)−\mathrm{1}}{{x}}=\mathrm{3} \\ $$
Answered by riyaziyyatelmlerinsahi last updated on 10/Sep/22
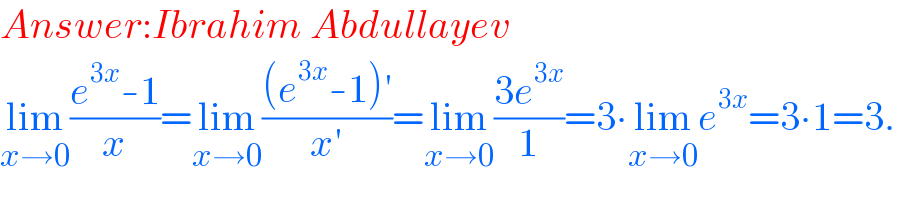
$${Answer}:{Ibrahim}\:{Abdullayev} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\mathrm{3}{x}} -\mathrm{1}}{{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({e}^{\mathrm{3}{x}} -\mathrm{1}\right)'}{{x}'}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}{e}^{\mathrm{3}{x}} }{\mathrm{1}}=\mathrm{3}\centerdot\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{e}^{\mathrm{3}{x}} =\mathrm{3}\centerdot\mathrm{1}=\mathrm{3}. \\ $$
