
Question Number 129387 by Study last updated on 15/Jan/21
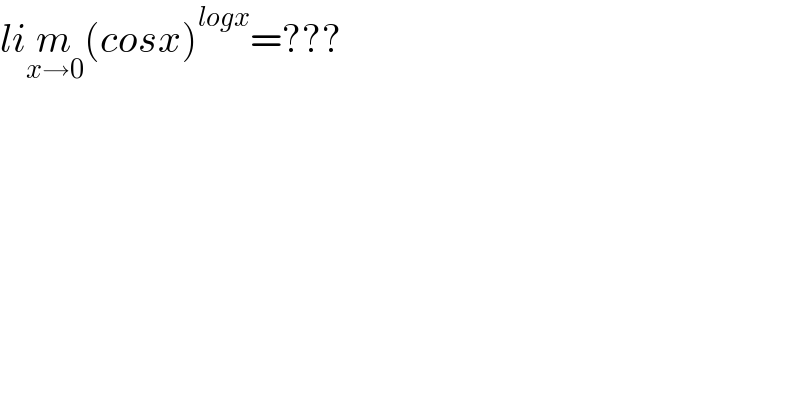
$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\left({cosx}\right)^{{logx}} =??? \\ $$
Commented by Study last updated on 15/Jan/21

$${who}\:{will}\:{solve}? \\ $$
Answered by mindispower last updated on 15/Jan/21
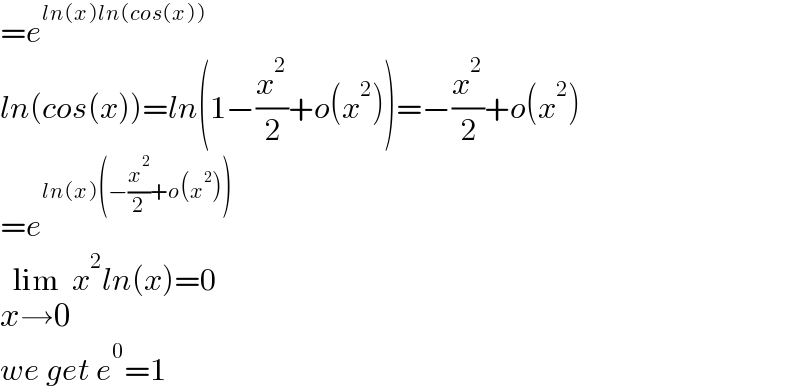
$$={e}^{{ln}\left({x}\right){ln}\left({cos}\left({x}\right)\right)} \\ $$$${ln}\left({cos}\left({x}\right)\right)={ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}^{\mathrm{2}} \right)\right)=−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$={e}^{{ln}\left({x}\right)\left(−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}^{\mathrm{2}} \right)\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{x}^{\mathrm{2}} {ln}\left({x}\right)=\mathrm{0} \\ $$$${we}\:{get}\:{e}^{\mathrm{0}} =\mathrm{1} \\ $$
Commented by Study last updated on 16/Jan/21
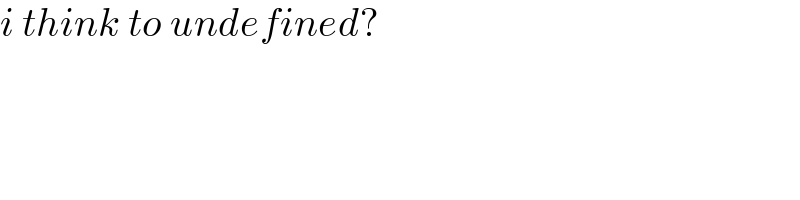
$${i}\:{think}\:{to}\:{undefined}? \\ $$
