
Question Number 129510 by Adel last updated on 16/Jan/21
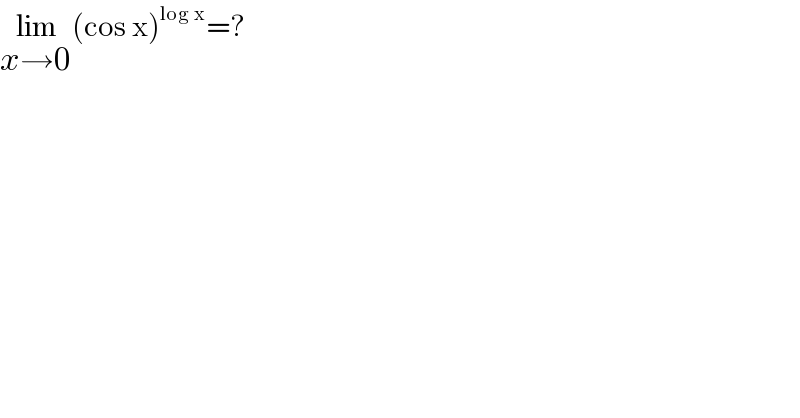
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{log}\:\mathrm{x}} =? \\ $$
Commented by mr W last updated on 16/Jan/21

$$\Rightarrow{Q}\mathrm{129387} \\ $$
Answered by greg_ed last updated on 16/Jan/21

$$\left(\boldsymbol{\mathrm{cos}}\:\boldsymbol{{x}}\right)^{\boldsymbol{{ln}}\:\boldsymbol{{x}}} \:=\:\boldsymbol{\mathrm{cos}}\:^{\boldsymbol{{ln}}\:\boldsymbol{{x}}\:} \boldsymbol{{x}}\:=\:\boldsymbol{{e}}\:^{\boldsymbol{{ln}}\:\boldsymbol{{x}}\:\boldsymbol{{ln}}\left(\boldsymbol{\mathrm{cos}}\:\boldsymbol{{x}}\right)} \\ $$$$\boldsymbol{\mathrm{let}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{rewrite}}\:\boldsymbol{\mathrm{this}}\:\boldsymbol{{u}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{ln}}\:\boldsymbol{{x}}\:\boldsymbol{{ln}}\left(\boldsymbol{\mathrm{cos}}\:\boldsymbol{{x}}\right). \\ $$$$\boldsymbol{{u}}\:\left(\boldsymbol{{x}}\right)=\frac{\boldsymbol{{ln}}\:\boldsymbol{{x}}}{\frac{\mathrm{1}}{\boldsymbol{{ln}}\left(\boldsymbol{\mathrm{cos}}\:\boldsymbol{{x}}\right)}} \\ $$$$ \\ $$$$\mathrm{1}.\:\boldsymbol{\mathrm{Applying}}\:\boldsymbol{\mathrm{L}}'\boldsymbol{\mathrm{Hopital}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{rule}},\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}}\: \\ $$$$\boldsymbol{{u}}\left(\boldsymbol{{x}}\right)=\frac{\boldsymbol{{ln}}\:^{\mathrm{2}} \:\left(\boldsymbol{\mathrm{cos}}\:\boldsymbol{{x}}\right)}{\boldsymbol{{x}}\:\boldsymbol{{tan}}\:\boldsymbol{{x}}} \\ $$$$\mathrm{2}.\:\boldsymbol{\mathrm{Applying}}\:\boldsymbol{\mathrm{L}}'\boldsymbol{\mathrm{Hopital}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{rule}},\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}} \\ $$$$\boldsymbol{{u}}\left(\boldsymbol{{x}}\right)=−\frac{\mathrm{2}\boldsymbol{{ln}}\left(\boldsymbol{\mathrm{cos}}\:\boldsymbol{{x}}\right)\boldsymbol{{tan}}\:\boldsymbol{{x}}}{\boldsymbol{{tan}}\:\boldsymbol{{x}}\:+\:\boldsymbol{{x}}\:\boldsymbol{{sec}}\:^{\mathrm{2}} \:\boldsymbol{{x}}} \\ $$$$\mathrm{3}.\:\boldsymbol{\mathrm{Applying}}\:\boldsymbol{\mathrm{L}}'\boldsymbol{\mathrm{Hopital}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{rule}},\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}} \\ $$$$\boldsymbol{{u}}\left(\boldsymbol{{x}}\right)=−\frac{−\boldsymbol{{tan}}\:^{\mathrm{2}} \:\boldsymbol{{x}}\:+\:\boldsymbol{\mathrm{sec}}\:^{\mathrm{2}} \:\boldsymbol{{x}}\:\boldsymbol{{ln}}\left(\boldsymbol{\mathrm{cos}}\:\boldsymbol{{x}}\right)}{\boldsymbol{\mathrm{sec}}\:^{\mathrm{2}} \:\boldsymbol{{x}}\:\left(\mathrm{1}+\:\boldsymbol{{x}}\:\boldsymbol{{tan}}\:\boldsymbol{{x}}\right)} \\ $$$$\boldsymbol{\mathrm{Plugging}}\:\boldsymbol{{x}}=\mathrm{0}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{this}},\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\boldsymbol{{u}}\left(\boldsymbol{{x}}\right)=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{So}},\:\boldsymbol{\mathrm{finally}}\: \\ $$$$\underset{\boldsymbol{{u}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\boldsymbol{{e}}\:^{\boldsymbol{{u}}\:} =\:\mathrm{1}.\: \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 16/Jan/21
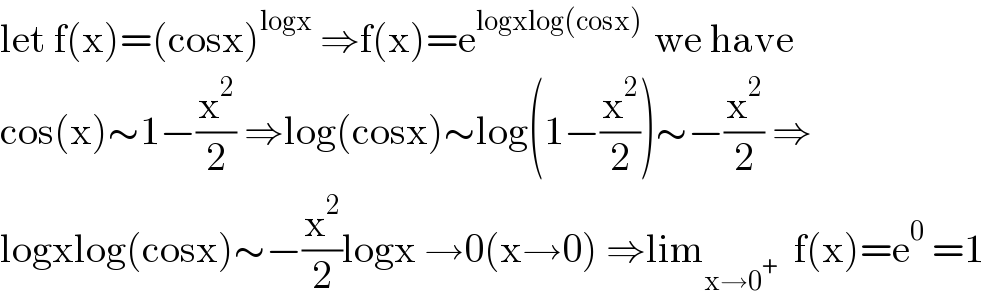
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{cosx}\right)^{\mathrm{logx}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{logxlog}\left(\mathrm{cosx}\right)\:} \:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{cos}\left(\mathrm{x}\right)\sim\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{log}\left(\mathrm{cosx}\right)\sim\mathrm{log}\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)\sim−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{logxlog}\left(\mathrm{cosx}\right)\sim−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{logx}\:\rightarrow\mathrm{0}\left(\mathrm{x}\rightarrow\mathrm{0}\right)\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{0}} \:=\mathrm{1} \\ $$
