
Question Number 101075 by bemath last updated on 30/Jun/20
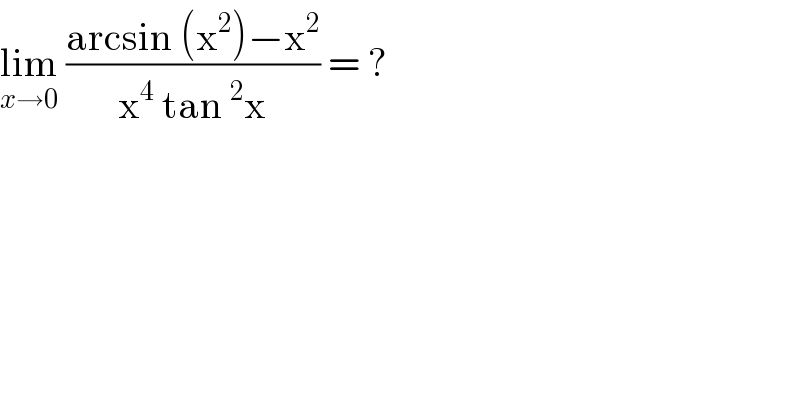
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{arcsin}\:\left(\mathrm{x}^{\mathrm{2}} \right)−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} \:\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\:=\:? \\ $$
Commented by Dwaipayan Shikari last updated on 30/Jun/20
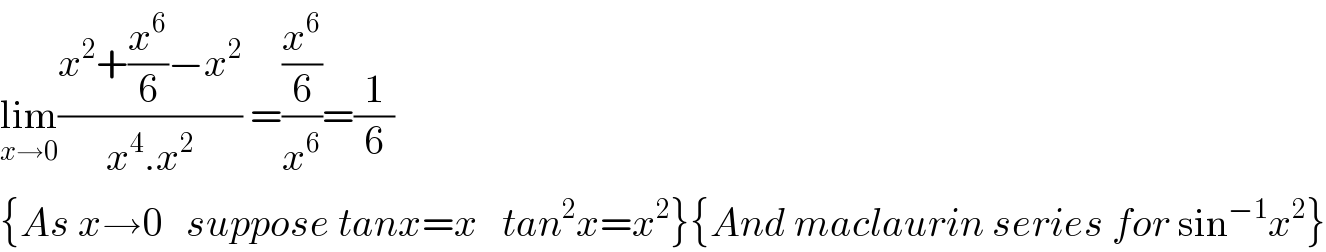
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{6}} }{\mathrm{6}}−{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} .{x}^{\mathrm{2}} }\:=\frac{\frac{{x}^{\mathrm{6}} }{\mathrm{6}}}{{x}^{\mathrm{6}} }=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\left\{{As}\:{x}\rightarrow\mathrm{0}\:\:\:{suppose}\:{tanx}={x}\:\:\:{tan}^{\mathrm{2}} {x}={x}^{\mathrm{2}} \right\}\left\{{And}\:{maclaurin}\:{series}\:{for}\:\mathrm{sin}^{−\mathrm{1}} {x}^{\mathrm{2}} \right\} \\ $$
