
Question Number 110132 by bemath last updated on 27/Aug/20
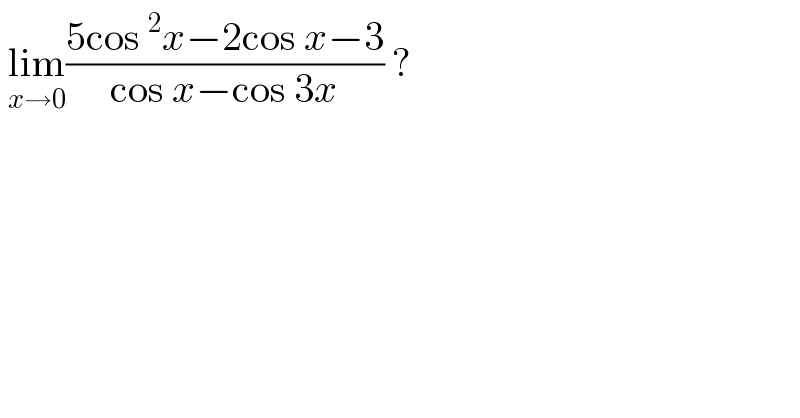
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{5cos}\:^{\mathrm{2}} {x}−\mathrm{2cos}\:{x}−\mathrm{3}}{\mathrm{cos}\:{x}−\mathrm{cos}\:\mathrm{3}{x}}\:? \\ $$
Commented by PRITHWISH SEN 2 last updated on 27/Aug/20

$$\mathrm{form}\:\frac{\mathrm{0}}{\mathrm{0}}\:\mathrm{use}\:\mathrm{L}'\mathrm{Hopital} \\ $$
Commented by bemath last updated on 27/Aug/20

Commented by bemath last updated on 27/Aug/20

$${yes}...{cooll} \\ $$
Commented by Dwaipayan Shikari last updated on 27/Aug/20
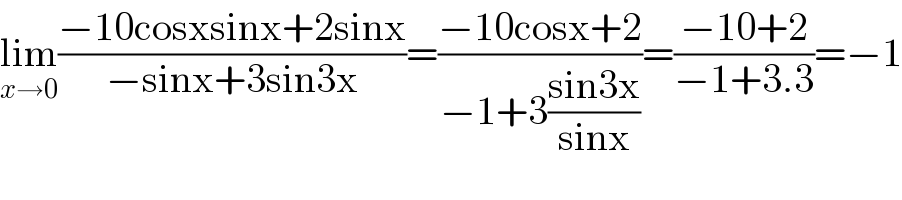
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{10cosxsinx}+\mathrm{2sinx}}{−\mathrm{sinx}+\mathrm{3sin3x}}=\frac{−\mathrm{10cosx}+\mathrm{2}}{−\mathrm{1}+\mathrm{3}\frac{\mathrm{sin3x}}{\mathrm{sinx}}}=\frac{−\mathrm{10}+\mathrm{2}}{−\mathrm{1}+\mathrm{3}.\mathrm{3}}=−\mathrm{1} \\ $$
