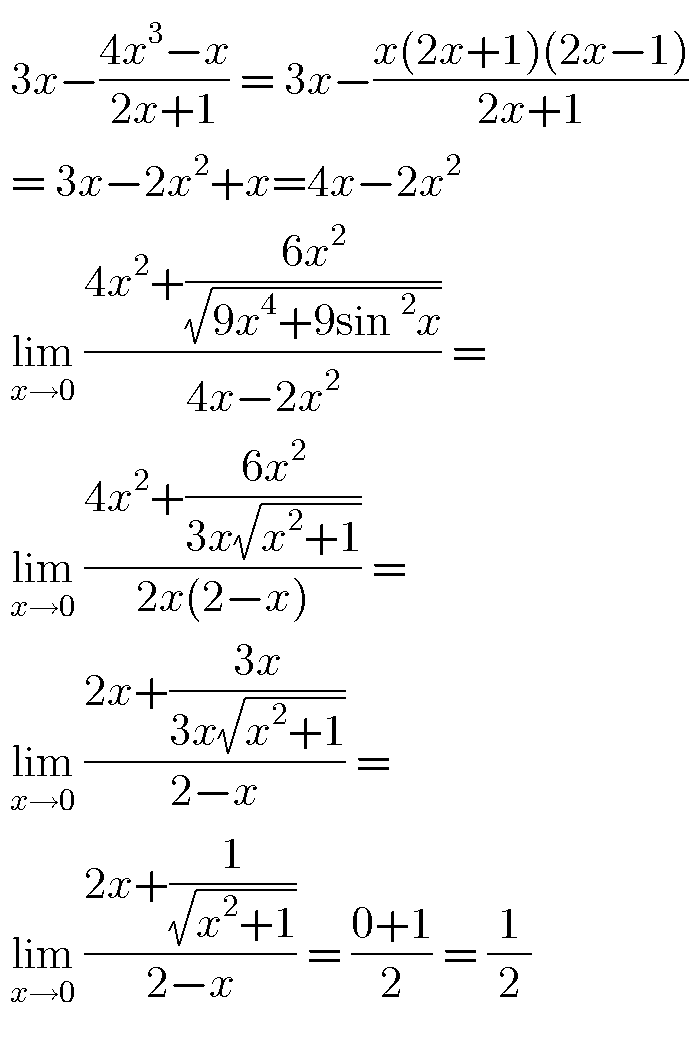Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 86193 by john santu last updated on 27/Mar/20

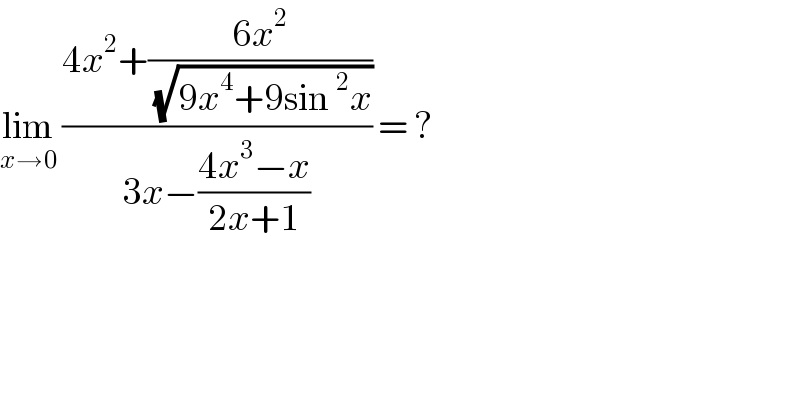
lim_(x→0) ((4x^2 +((6x^2 )/(√(9x^4 +9sin^2 x))))/(3x−((4x^3 −x)/(2x+1)))) = ?

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4}{x}^{\mathrm{2}} +\frac{\mathrm{6}{x}^{\mathrm{2}} }{\sqrt{\mathrm{9}{x}^{\mathrm{4}} +\mathrm{9sin}\:^{\mathrm{2}} {x}}}}{\mathrm{3}{x}−\frac{\mathrm{4}{x}^{\mathrm{3}} −{x}}{\mathrm{2}{x}+\mathrm{1}}}\:=\:? \\ $$

Commented by jagoll last updated on 27/Mar/20

i like this question

$$\mathrm{i}\:\mathrm{like}\:\mathrm{this}\:\mathrm{question} \\ $$

Commented by MJS last updated on 27/Mar/20

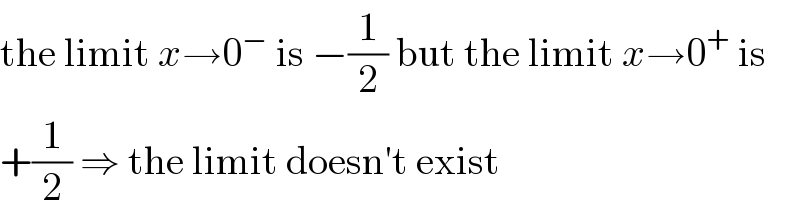
the limit x→0^− is −(1/2) but the limit x→0^+ is +(1/2) ⇒ the limit doesn′t exist

$$\mathrm{the}\:\mathrm{limit}\:{x}\rightarrow\mathrm{0}^{−} \:\mathrm{is}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{but}\:\mathrm{the}\:\mathrm{limit}\:{x}\rightarrow\mathrm{0}^{+} \:\mathrm{is} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:\mathrm{the}\:\mathrm{limit}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$

Commented by MJS last updated on 28/Mar/20

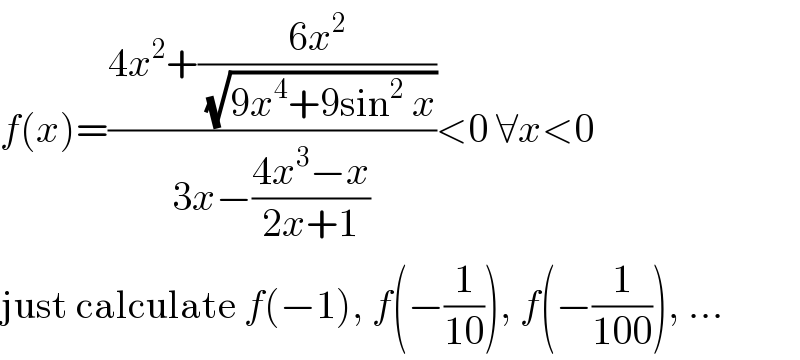
f(x)=((4x^2 +((6x^2 )/(√(9x^4 +9sin^2 x))))/(3x−((4x^3 −x)/(2x+1))))<0 ∀x<0 just calculate f(−1), f(−(1/(10))), f(−(1/(100))), ...

$${f}\left({x}\right)=\frac{\mathrm{4}{x}^{\mathrm{2}} +\frac{\mathrm{6}{x}^{\mathrm{2}} }{\sqrt{\mathrm{9}{x}^{\mathrm{4}} +\mathrm{9sin}^{\mathrm{2}} \:{x}}}}{\mathrm{3}{x}−\frac{\mathrm{4}{x}^{\mathrm{3}} −{x}}{\mathrm{2}{x}+\mathrm{1}}}<\mathrm{0}\:\forall{x}<\mathrm{0} \\ $$$$\mathrm{just}\:\mathrm{calculate}\:{f}\left(−\mathrm{1}\right),\:{f}\left(−\frac{\mathrm{1}}{\mathrm{10}}\right),\:{f}\left(−\frac{\mathrm{1}}{\mathrm{100}}\right),\:... \\ $$

Commented by john santu last updated on 28/Mar/20

post your argument sir

$${post}\:{your}\:{argument}\:{sir} \\ $$

Commented by jagoll last updated on 28/Mar/20

why?

$$\mathrm{why}? \\ $$$$ \\ $$

Commented by john santu last updated on 28/Mar/20

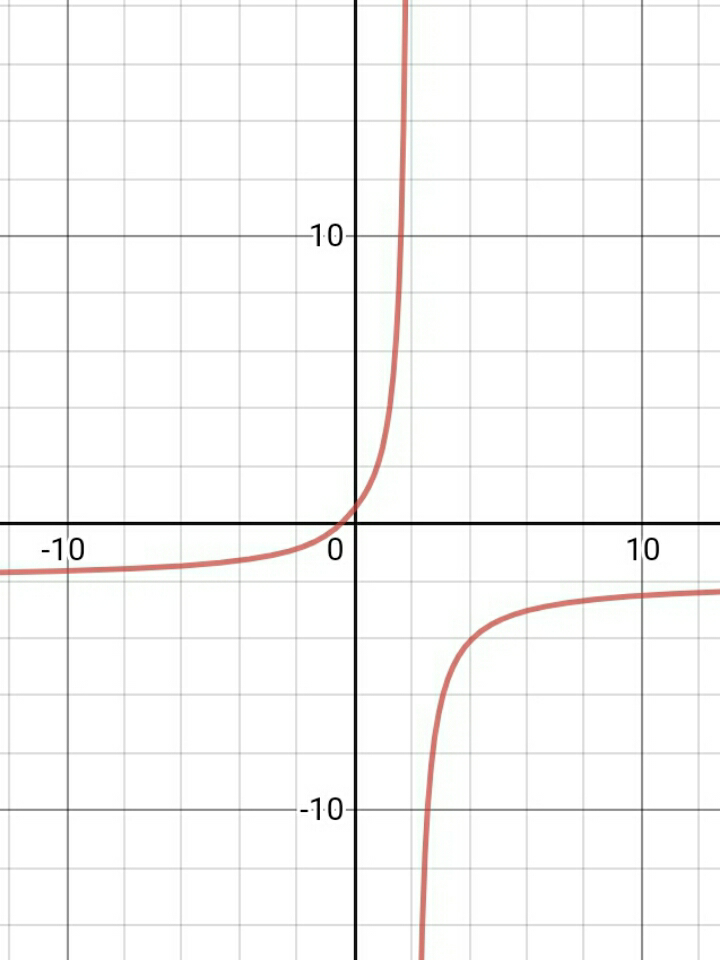
Commented by john santu last updated on 28/Mar/20

this the graph?

$${this}\:{the}\:{graph}?\: \\ $$

Commented by MJS last updated on 28/Mar/20

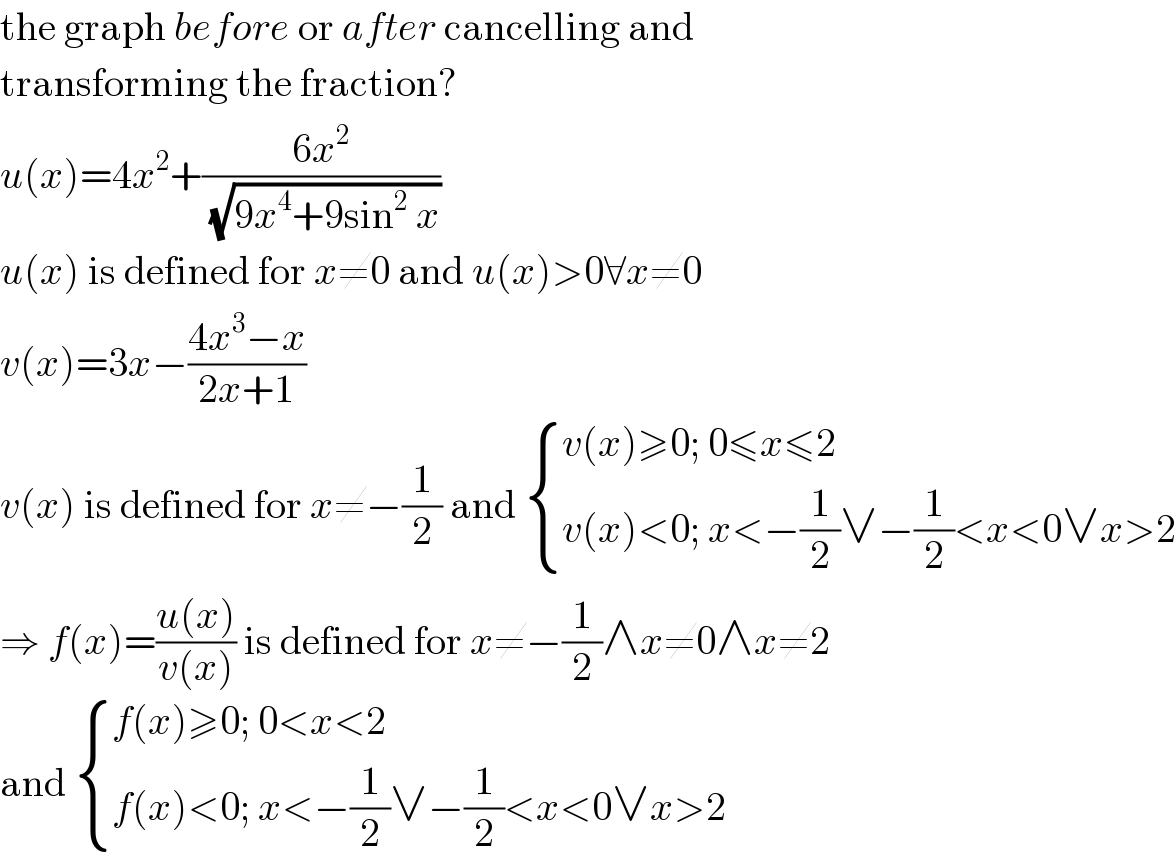
the graph before or after cancelling and transforming the fraction? u(x)=4x^2 +((6x^2 )/(√(9x^4 +9sin^2 x))) u(x) is defined for x≠0 and u(x)>0∀x≠0 v(x)=3x−((4x^3 −x)/(2x+1)) v(x) is defined for x≠−(1/2) and { ((v(x)≥0; 0≤x≤2)),((v(x)<0; x<−(1/2)∨−(1/2)<x<0∨x>2)) :} ⇒ f(x)=((u(x))/(v(x))) is defined for x≠−(1/2)∧x≠0∧x≠2 and { ((f(x)≥0; 0<x<2)),((f(x)<0; x<−(1/2)∨−(1/2)<x<0∨x>2)) :}

$$\mathrm{the}\:\mathrm{graph}\:{before}\:\mathrm{or}\:{after}\:\mathrm{cancelling}\:\mathrm{and} \\ $$$$\mathrm{transforming}\:\mathrm{the}\:\mathrm{fraction}? \\ $$$${u}\left({x}\right)=\mathrm{4}{x}^{\mathrm{2}} +\frac{\mathrm{6}{x}^{\mathrm{2}} }{\sqrt{\mathrm{9}{x}^{\mathrm{4}} +\mathrm{9sin}^{\mathrm{2}} \:{x}}} \\ $$$${u}\left({x}\right)\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:{x}\neq\mathrm{0}\:\mathrm{and}\:{u}\left({x}\right)>\mathrm{0}\forall{x}\neq\mathrm{0} \\ $$$${v}\left({x}\right)=\mathrm{3}{x}−\frac{\mathrm{4}{x}^{\mathrm{3}} −{x}}{\mathrm{2}{x}+\mathrm{1}} \\ $$$${v}\left({x}\right)\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:{x}\neq−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:\begin{cases}{{v}\left({x}\right)\geqslant\mathrm{0};\:\mathrm{0}\leqslant{x}\leqslant\mathrm{2}}\\{{v}\left({x}\right)<\mathrm{0};\:{x}<−\frac{\mathrm{1}}{\mathrm{2}}\vee−\frac{\mathrm{1}}{\mathrm{2}}<{x}<\mathrm{0}\vee{x}>\mathrm{2}}\end{cases} \\ $$$$\Rightarrow\:{f}\left({x}\right)=\frac{{u}\left({x}\right)}{{v}\left({x}\right)}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:{x}\neq−\frac{\mathrm{1}}{\mathrm{2}}\wedge{x}\neq\mathrm{0}\wedge{x}\neq\mathrm{2} \\ $$$$\mathrm{and}\:\begin{cases}{{f}\left({x}\right)\geqslant\mathrm{0};\:\mathrm{0}<{x}<\mathrm{2}}\\{{f}\left({x}\right)<\mathrm{0};\:{x}<−\frac{\mathrm{1}}{\mathrm{2}}\vee−\frac{\mathrm{1}}{\mathrm{2}}<{x}<\mathrm{0}\vee{x}>\mathrm{2}}\end{cases} \\ $$

Answered by john santu last updated on 27/Mar/20

Terms of Service

Privacy Policy

Contact: info@tinkutara.com