Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 147169 by mathdanisur last updated on 18/Jul/21

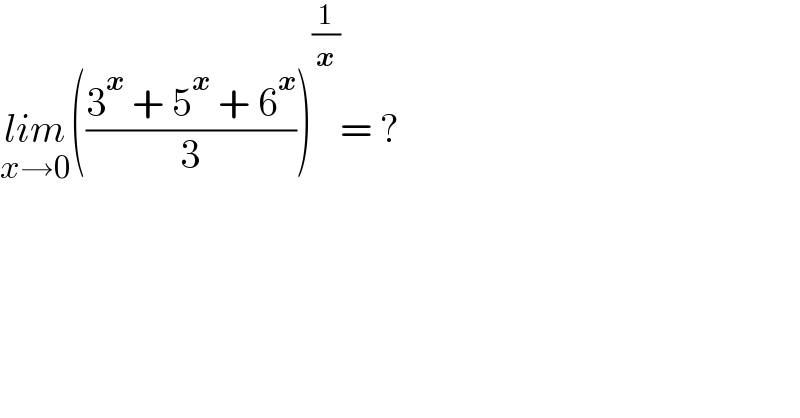
lim_(x→0) (((3^x + 5^x + 6^x )/3))^(1/x) = ?

$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\left(\frac{\mathrm{3}^{\boldsymbol{{x}}} \:+\:\mathrm{5}^{\boldsymbol{{x}}} \:+\:\mathrm{6}^{\boldsymbol{{x}}} }{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\boldsymbol{{x}}}} =\:? \\ $$

Commented by gsk2684 last updated on 18/Jul/21

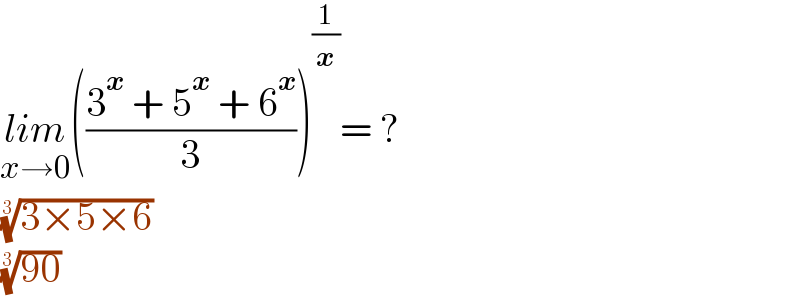
lim_(x→0) (((3^x + 5^x + 6^x )/3))^(1/x) = ? ((3×5×6))^(1/3) ((90))^(1/3)

$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\left(\frac{\mathrm{3}^{\boldsymbol{{x}}} \:+\:\mathrm{5}^{\boldsymbol{{x}}} \:+\:\mathrm{6}^{\boldsymbol{{x}}} }{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\boldsymbol{{x}}}} =\:? \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{3}×\mathrm{5}×\mathrm{6}} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{90}} \\ $$

Commented by mathdanisur last updated on 19/Jul/21

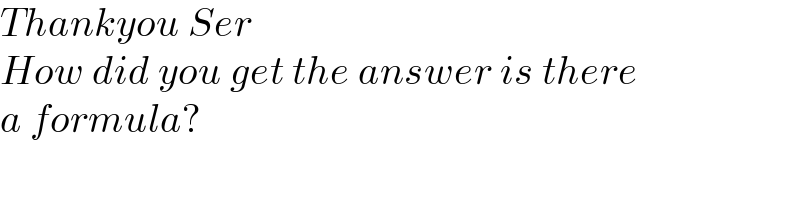
Thankyou Ser How did you get the answer is there a formula?

$${Thankyou}\:{Ser} \\ $$$${How}\:{did}\:{you}\:{get}\:{the}\:{answer}\:{is}\:{there} \\ $$$${a}\:{formula}? \\ $$

Commented by gsk2684 last updated on 21/Jul/21

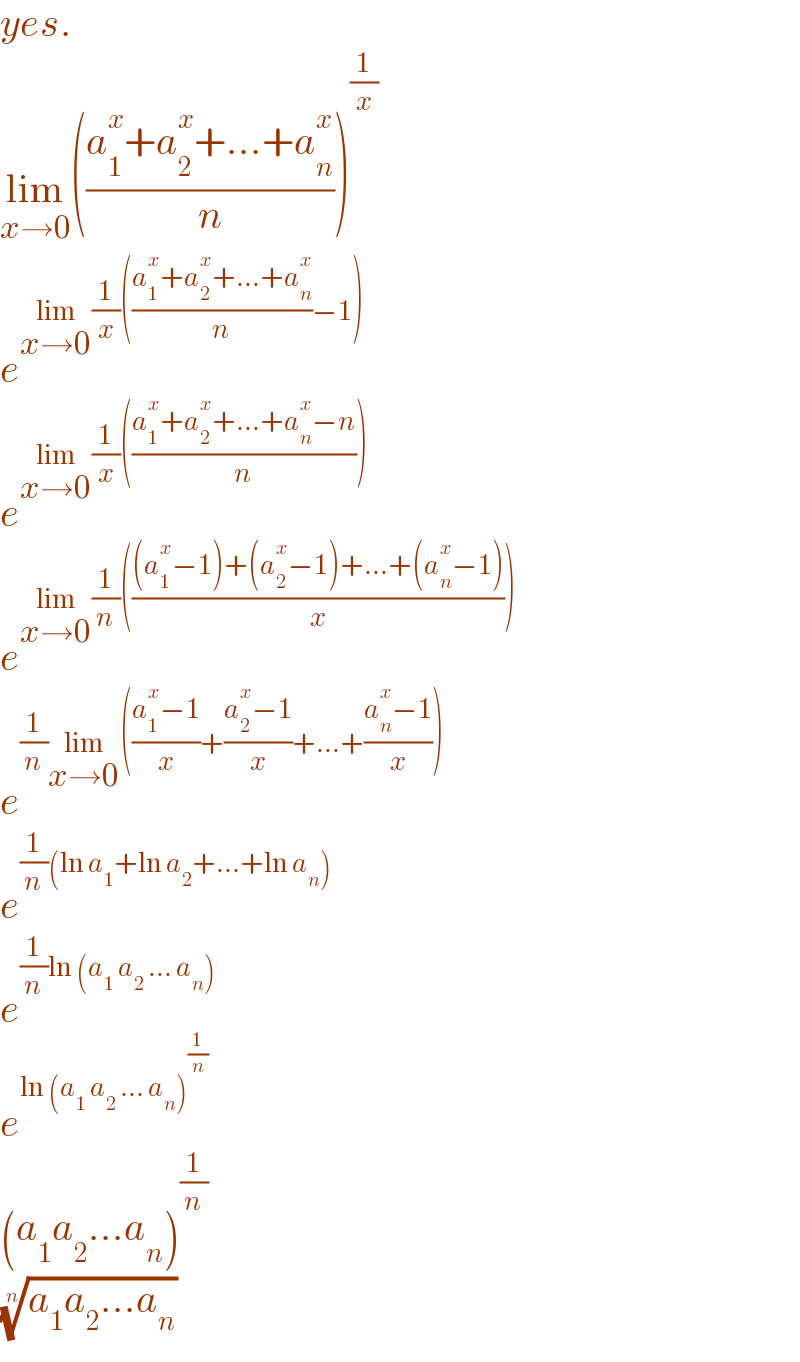
yes. lim_(x→0) (((a_1 ^x +a_2 ^x +...+a_n ^x )/n))^(1/x) e^(lim_(x→0) (1/x)(((a_1 ^x +a_2 ^x +...+a_n ^x )/n)−1)) e^(lim_(x→0) (1/x)(((a_1 ^x +a_2 ^x +...+a_n ^x −n)/n))) e^(lim_(x→0) (1/n)((((a_1 ^x −1)+(a_2 ^x −1)+...+(a_n ^x −1))/x))) e^((1/n)lim_(x→0) (((a_1 ^x −1)/x)+((a_2 ^x −1)/x)+...+((a_n ^x −1)/x))) e^((1/n)(ln a_1 +ln a_2 +...+ln a_n )) e^((1/n)ln (a_1 a_2 ... a_n )) e^(ln (a_1 a_2 ... a_n )^(1/n) ) (a_1 a_2 ...a_n )^(1/n) ((a_1 a_2 ...a_n ))^(1/n)

$${yes}. \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{a}_{\mathrm{1}} ^{{x}} +{a}_{\mathrm{2}} ^{{x}} +...+{a}_{{n}} ^{{x}} }{{n}}\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}\left(\frac{{a}_{\mathrm{1}} ^{{x}} +{a}_{\mathrm{2}} ^{{x}} +...+{a}_{{n}} ^{{x}} }{{n}}−\mathrm{1}\right)} \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}\left(\frac{{a}_{\mathrm{1}} ^{{x}} +{a}_{\mathrm{2}} ^{{x}} +...+{a}_{{n}} ^{{x}} −{n}}{{n}}\right)} \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\left(\frac{\left({a}_{\mathrm{1}} ^{{x}} −\mathrm{1}\right)+\left({a}_{\mathrm{2}} ^{{x}} −\mathrm{1}\right)+...+\left({a}_{{n}} ^{{x}} −\mathrm{1}\right)}{{x}}\right)} \\ $$$${e}^{\frac{\mathrm{1}}{{n}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{a}_{\mathrm{1}} ^{{x}} −\mathrm{1}}{{x}}+\frac{{a}_{\mathrm{2}} ^{{x}} −\mathrm{1}}{{x}}+...+\frac{{a}_{{n}} ^{{x}} −\mathrm{1}}{{x}}\right)} \\ $$$${e}^{\frac{\mathrm{1}}{{n}}\left(\mathrm{ln}\:{a}_{\mathrm{1}} +\mathrm{ln}\:{a}_{\mathrm{2}} +...+\mathrm{ln}\:{a}_{{n}} \right)} \\ $$$${e}^{\frac{\mathrm{1}}{{n}}\mathrm{ln}\:\left({a}_{\mathrm{1}} \:{a}_{\mathrm{2}} \:...\:{a}_{{n}} \right)} \\ $$$${e}^{\mathrm{ln}\:\left({a}_{\mathrm{1}} \:{a}_{\mathrm{2}} \:...\:{a}_{{n}} \right)^{\frac{\mathrm{1}}{{n}}} } \\ $$$$\left({a}_{\mathrm{1}} {a}_{\mathrm{2}} ...{a}_{{n}} \right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$\sqrt[{{n}}]{{a}_{\mathrm{1}} {a}_{\mathrm{2}} ...{a}_{{n}} } \\ $$

Commented by mathdanisur last updated on 21/Jul/21

Thank you Ser, cool

$${Thank}\:{you}\:{Ser},\:{cool} \\ $$

Answered by mathmax by abdo last updated on 18/Jul/21

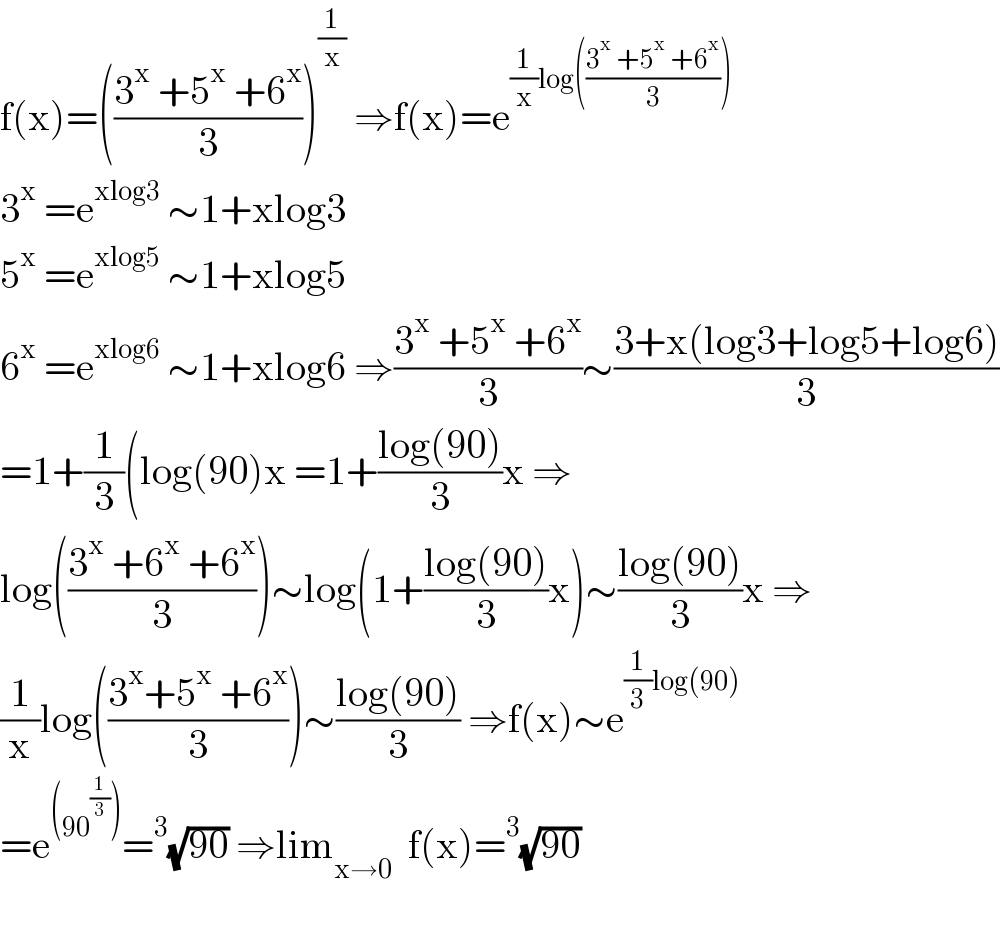
f(x)=(((3^x +5^x +6^x )/3))^(1/x) ⇒f(x)=e^((1/x)log(((3^(x ) +5^x +6^x )/3))) 3^x =e^(xlog3) ∼1+xlog3 5^x =e^(xlog5) ∼1+xlog5 6^x =e^(xlog6) ∼1+xlog6 ⇒((3^x +5^x +6^x )/3)∼((3+x(log3+log5+log6))/3) =1+(1/3)(log(90)x =1+((log(90))/3)x ⇒ log(((3^x +6^x +6^x )/3))∼log(1+((log(90))/3)x)∼((log(90))/3)x ⇒ (1/x)log(((3^x +5^x +6^x )/3))∼((log(90))/3) ⇒f(x)∼e^((1/3)log(90)) =e^((90^(1/3) )) =^3 (√(90)) ⇒lim_(x→0) f(x)=^3 (√(90))

$$\mathrm{f}\left(\mathrm{x}\right)=\left(\frac{\mathrm{3}^{\mathrm{x}} \:+\mathrm{5}^{\mathrm{x}} \:+\mathrm{6}^{\mathrm{x}} }{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}\mathrm{log}\left(\frac{\mathrm{3}^{\mathrm{x}\:} +\mathrm{5}^{\mathrm{x}} \:+\mathrm{6}^{\mathrm{x}} }{\mathrm{3}}\right)} \\ $$$$\mathrm{3}^{\mathrm{x}} \:=\mathrm{e}^{\mathrm{xlog3}} \:\sim\mathrm{1}+\mathrm{xlog3} \\ $$$$\mathrm{5}^{\mathrm{x}} \:=\mathrm{e}^{\mathrm{xlog5}} \:\sim\mathrm{1}+\mathrm{xlog5} \\ $$$$\mathrm{6}^{\mathrm{x}} \:=\mathrm{e}^{\mathrm{xlog6}} \:\sim\mathrm{1}+\mathrm{xlog6}\:\Rightarrow\frac{\mathrm{3}^{\mathrm{x}} \:+\mathrm{5}^{\mathrm{x}} \:+\mathrm{6}^{\mathrm{x}} }{\mathrm{3}}\sim\frac{\mathrm{3}+\mathrm{x}\left(\mathrm{log3}+\mathrm{log5}+\mathrm{log6}\right)}{\mathrm{3}} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{log}\left(\mathrm{90}\right)\mathrm{x}\:=\mathrm{1}+\frac{\mathrm{log}\left(\mathrm{90}\right)}{\mathrm{3}}\mathrm{x}\:\Rightarrow\right. \\ $$$$\mathrm{log}\left(\frac{\mathrm{3}^{\mathrm{x}} \:+\mathrm{6}^{\mathrm{x}} \:+\mathrm{6}^{\mathrm{x}} }{\mathrm{3}}\right)\sim\mathrm{log}\left(\mathrm{1}+\frac{\mathrm{log}\left(\mathrm{90}\right)}{\mathrm{3}}\mathrm{x}\right)\sim\frac{\mathrm{log}\left(\mathrm{90}\right)}{\mathrm{3}}\mathrm{x}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}\mathrm{log}\left(\frac{\mathrm{3}^{\mathrm{x}} +\mathrm{5}^{\mathrm{x}} \:+\mathrm{6}^{\mathrm{x}} }{\mathrm{3}}\right)\sim\frac{\mathrm{log}\left(\mathrm{90}\right)}{\mathrm{3}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}\left(\mathrm{90}\right)} \\ $$$$=\mathrm{e}^{\left(\mathrm{90}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)} =^{\mathrm{3}} \sqrt{\mathrm{90}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\mathrm{f}\left(\mathrm{x}\right)=^{\mathrm{3}} \sqrt{\mathrm{90}} \\ $$$$ \\ $$

Commented by mathdanisur last updated on 19/Jul/21

thank you Ser

$${thank}\:{you}\:{Ser} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com