Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 115616 by bobhans last updated on 27/Sep/20

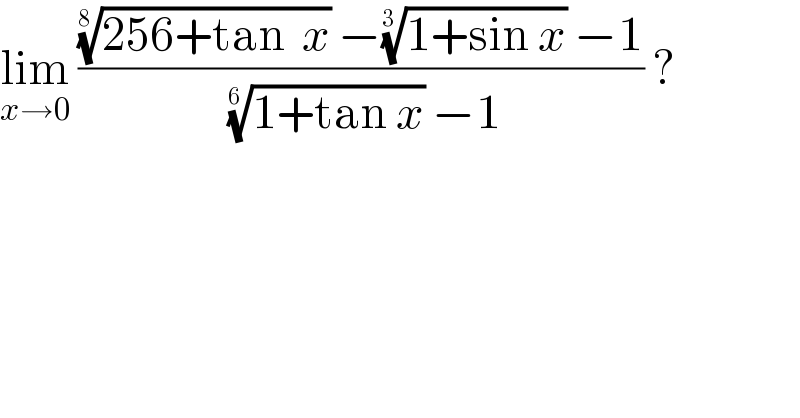
lim_(x→0) ((((256+tan x))^(1/(8 )) −((1+sin x))^(1/(3 )) −1)/( ((1+tan x))^(1/(6 )) −1)) ?

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{8}\:}]{\mathrm{256}+\mathrm{tan}\:\:{x}}\:−\sqrt[{\mathrm{3}\:}]{\mathrm{1}+\mathrm{sin}\:{x}}\:−\mathrm{1}}{\:\sqrt[{\mathrm{6}\:}]{\mathrm{1}+\mathrm{tan}\:{x}}\:−\mathrm{1}}\:? \\ $$

Answered by john santu last updated on 27/Sep/20

lim_(x→0) ((2 ((1+((tan x)/(256))))^(1/(8 )) −((1+sin x))^(1/(3 )) −1)/( ((1+tan x))^(1/(6 )) −1)) = lim_(x→0) ((2(1+(x/(8×256)))−(1+(x/3))−1)/((1+(x/6))−1)) = lim_(x→0) ((x((1/(4×256)) −(1/3)))/(x/6)) = 6.((1/(4×256)) −(1/3)) = (3/(2×256)) − 2 = (3/(512)) −2 = −((1021)/(512))

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\:\sqrt[{\mathrm{8}\:}]{\mathrm{1}+\frac{\mathrm{tan}\:{x}}{\mathrm{256}}}−\sqrt[{\mathrm{3}\:}]{\mathrm{1}+\mathrm{sin}\:{x}}\:−\mathrm{1}}{\:\sqrt[{\mathrm{6}\:}]{\mathrm{1}+\mathrm{tan}\:{x}}\:−\mathrm{1}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left(\mathrm{1}+\frac{{x}}{\mathrm{8}×\mathrm{256}}\right)−\left(\mathrm{1}+\frac{{x}}{\mathrm{3}}\right)−\mathrm{1}}{\left(\mathrm{1}+\frac{{x}}{\mathrm{6}}\right)−\mathrm{1}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\left(\frac{\mathrm{1}}{\mathrm{4}×\mathrm{256}}\:−\frac{\mathrm{1}}{\mathrm{3}}\right)}{\frac{{x}}{\mathrm{6}}}\:=\:\mathrm{6}.\left(\frac{\mathrm{1}}{\mathrm{4}×\mathrm{256}}\:−\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{2}×\mathrm{256}}\:−\:\mathrm{2}\:=\:\frac{\mathrm{3}}{\mathrm{512}}\:−\mathrm{2}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\frac{\mathrm{1021}}{\mathrm{512}} \\ $$

Answered by Dwaipayan Shikari last updated on 27/Sep/20

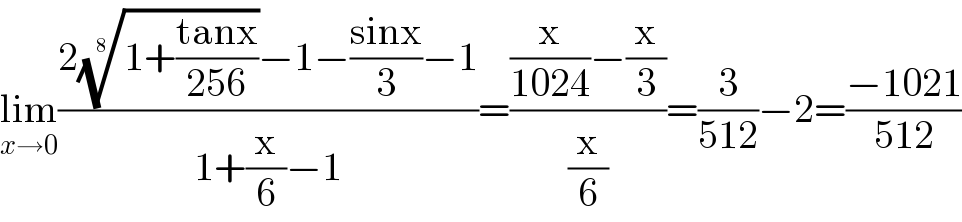
lim_(x→0) ((2((1+((tanx)/(256))))^(1/8) −1−((sinx)/3)−1)/(1+(x/6)−1))=(((x/(1024))−(x/3))/(x/6))=(3/(512))−2=((−1021)/(512))

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\sqrt[{\mathrm{8}}]{\mathrm{1}+\frac{\mathrm{tanx}}{\mathrm{256}}}−\mathrm{1}−\frac{\mathrm{sinx}}{\mathrm{3}}−\mathrm{1}}{\mathrm{1}+\frac{\mathrm{x}}{\mathrm{6}}−\mathrm{1}}=\frac{\frac{\mathrm{x}}{\mathrm{1024}}−\frac{\mathrm{x}}{\mathrm{3}}}{\frac{\mathrm{x}}{\mathrm{6}}}=\frac{\mathrm{3}}{\mathrm{512}}−\mathrm{2}=\frac{−\mathrm{1021}}{\mathrm{512}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com