Question Number 99720 by bobhans last updated on 23/Jun/20
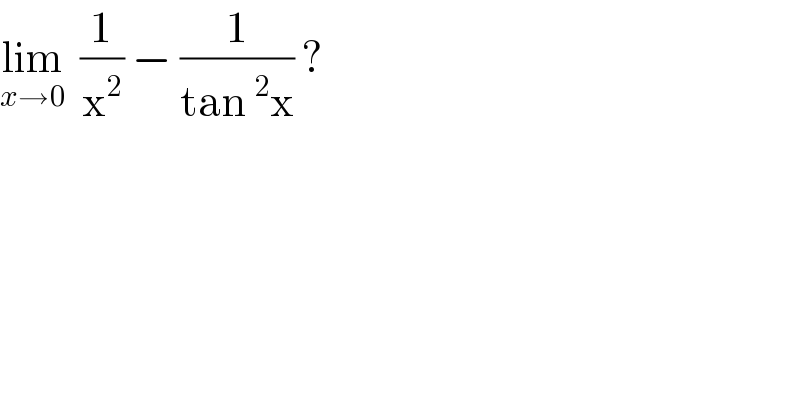
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\:? \\ $$
Commented by john santu last updated on 23/Jun/20
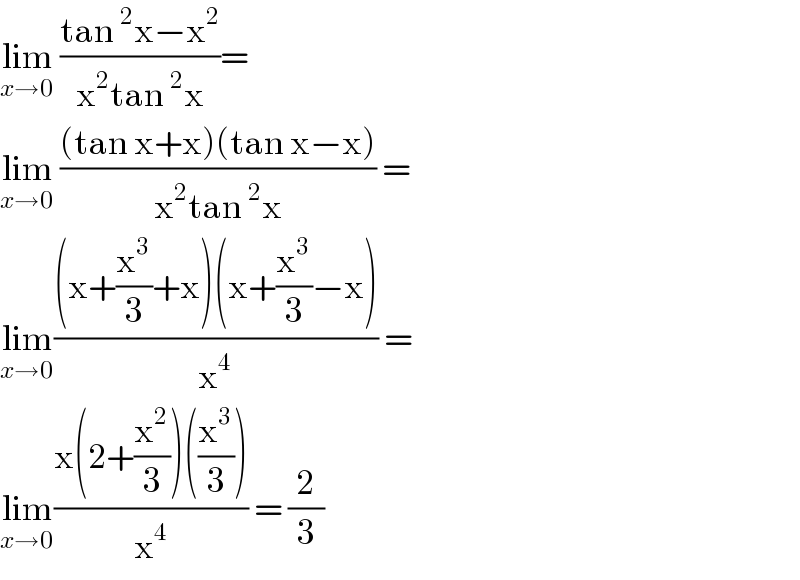
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{tan}\:\mathrm{x}+\mathrm{x}\right)\left(\mathrm{tan}\:\mathrm{x}−\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{x}\right)\left(\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}\left(\mathrm{2}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}\right)\left(\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\right)}{\mathrm{x}^{\mathrm{4}} }\:=\:\frac{\mathrm{2}}{\mathrm{3}}\: \\ $$
Commented by mr W last updated on 23/Jun/20
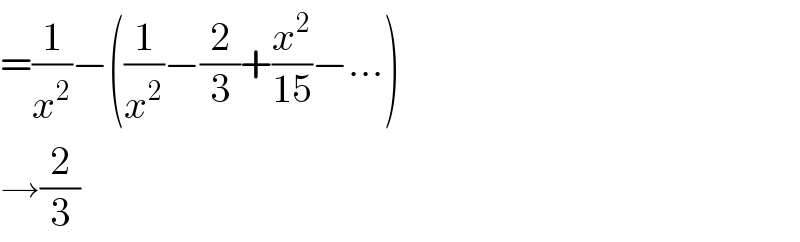
$$=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{3}}+\frac{{x}^{\mathrm{2}} }{\mathrm{15}}−...\right) \\ $$$$\rightarrow\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by john santu last updated on 23/Jun/20

$$\mathrm{joos}...\mathrm{tooss}\:\mathrm{prof}\:\mathrm{W} \\ $$
Commented by bobhans last updated on 24/Jun/20
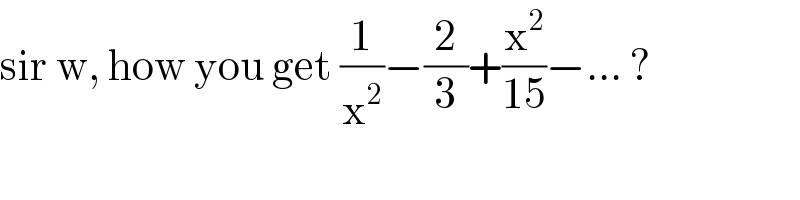
$$\mathrm{sir}\:\mathrm{w},\:\mathrm{how}\:\mathrm{you}\:\mathrm{get}\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{15}}−...\:?\: \\ $$
Commented by mr W last updated on 24/Jun/20
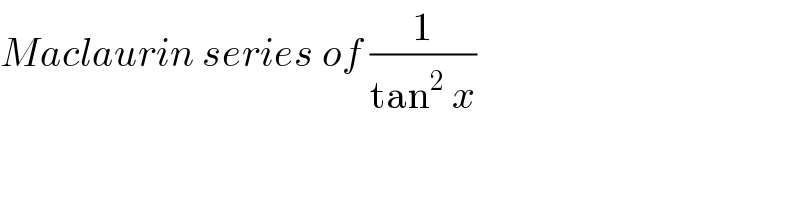
$${Maclaurin}\:{series}\:{of}\:\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:{x}} \\ $$
Answered by Ar Brandon last updated on 23/Jun/20
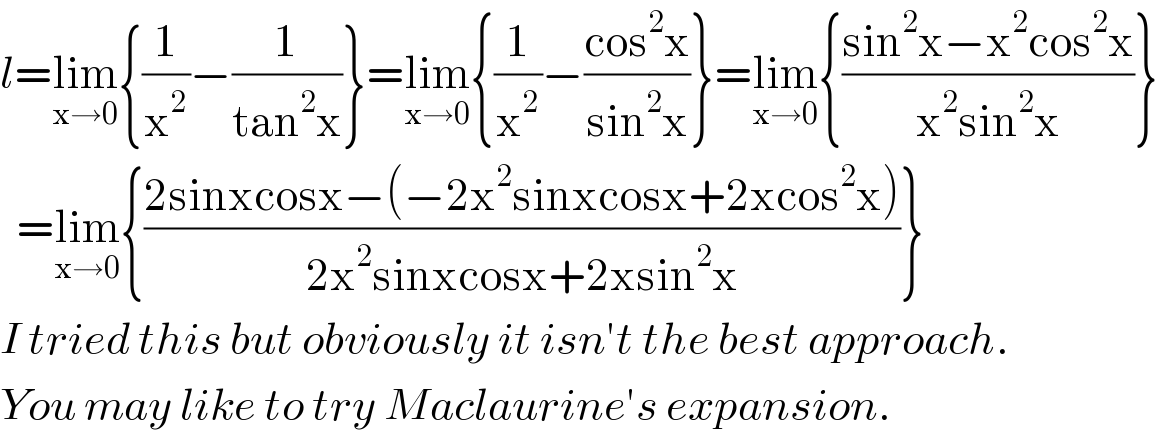
$${l}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \mathrm{x}}\right\}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\right\}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{x}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}}\right\} \\ $$$$\:\:=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{\mathrm{2sinxcosx}−\left(−\mathrm{2x}^{\mathrm{2}} \mathrm{sinxcosx}+\mathrm{2xcos}^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{2x}^{\mathrm{2}} \mathrm{sinxcosx}+\mathrm{2xsin}^{\mathrm{2}} \mathrm{x}}\right\} \\ $$$${I}\:{tried}\:{this}\:{but}\:{obviously}\:{it}\:{isn}'{t}\:{the}\:{best}\:{approach}. \\ $$$${You}\:{may}\:{like}\:{to}\:{try}\:{Maclaurine}'{s}\:{expansion}. \\ $$
Commented by bobhans last updated on 23/Jun/20
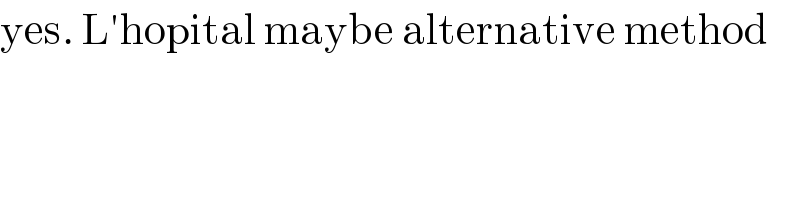
$$\mathrm{yes}.\:\mathrm{L}'\mathrm{hopital}\:\mathrm{maybe}\:\mathrm{alternative}\:\mathrm{method} \\ $$
Answered by john santu last updated on 23/Jun/20