
Question Number 199843 by universe last updated on 10/Nov/23
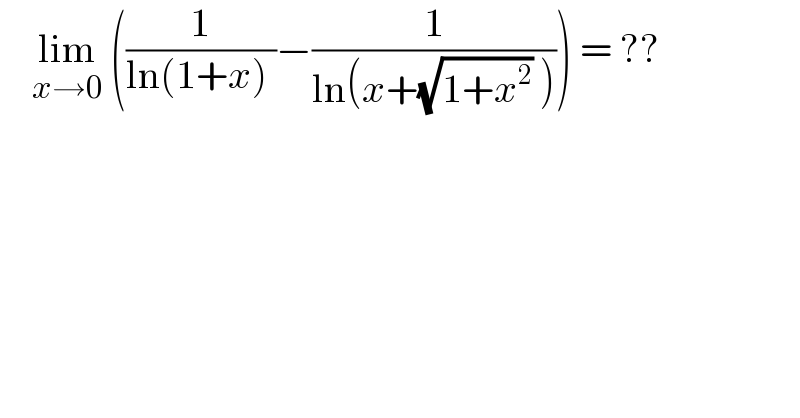
$$\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{ln}\left(\mathrm{1}+{x}\right)\:}−\frac{\mathrm{1}}{\mathrm{ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)}\right)\:=\:?? \\ $$
Answered by witcher3 last updated on 10/Nov/23
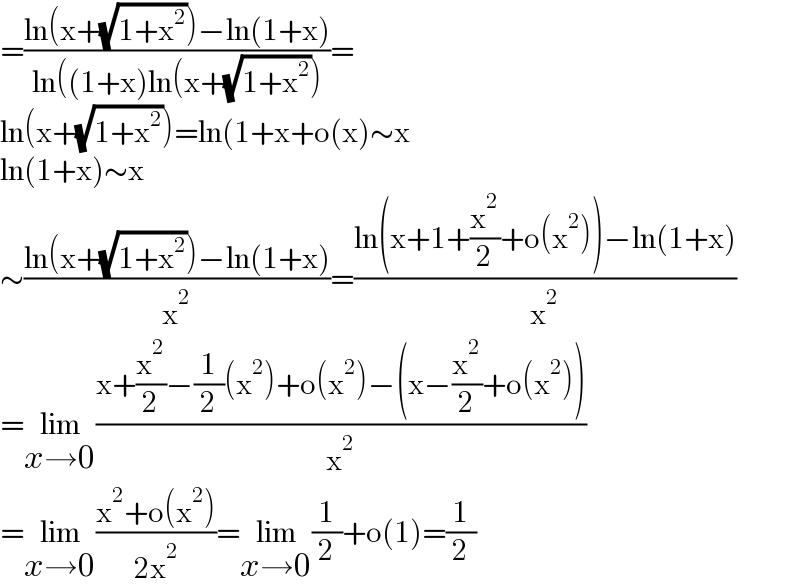
$$=\frac{\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{ln}\left(\left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\right.}= \\ $$$$\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)=\mathrm{ln}\left(\mathrm{1}+\mathrm{x}+\mathrm{o}\left(\mathrm{x}\right)\sim\mathrm{x}\right. \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\sim\mathrm{x} \\ $$$$\sim\frac{\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{ln}\left(\mathrm{x}+\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)\right)−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}^{\mathrm{2}} \right)+\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)−\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)\right)}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{2x}^{\mathrm{2}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{o}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
