
Question Number 159646 by cortano last updated on 19/Nov/21
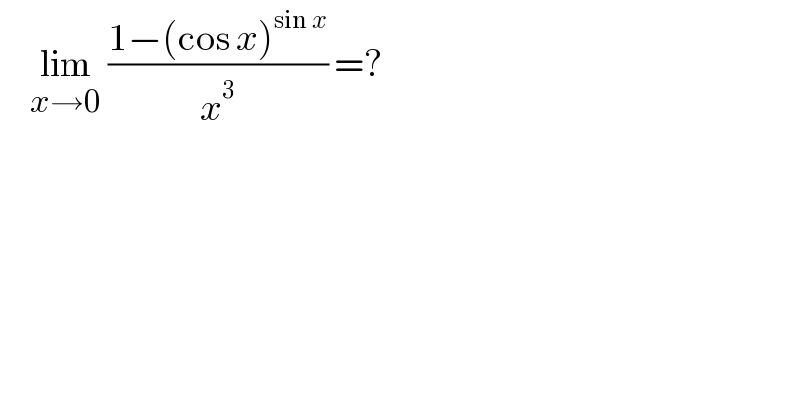
$$\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{cos}\:{x}\right)^{\mathrm{sin}\:{x}} }{{x}^{\mathrm{3}} }\:=? \\ $$
Answered by FongXD last updated on 19/Nov/21
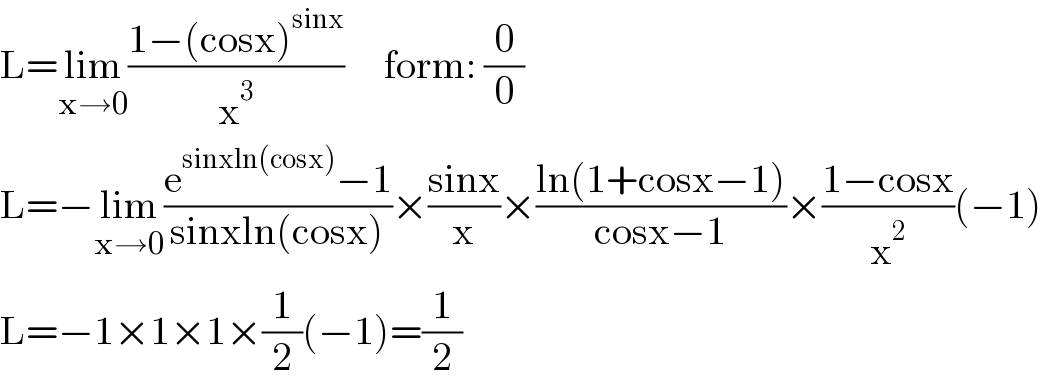
$$\mathrm{L}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\left(\mathrm{cosx}\right)^{\mathrm{sinx}} }{\mathrm{x}^{\mathrm{3}} }\:\:\:\:\:\mathrm{form}:\:\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\mathrm{L}=−\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{e}^{\mathrm{sinxln}\left(\mathrm{cosx}\right)} −\mathrm{1}}{\mathrm{sinxln}\left(\mathrm{cosx}\right)}×\frac{\mathrm{sinx}}{\mathrm{x}}×\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{cosx}−\mathrm{1}\right)}{\mathrm{cosx}−\mathrm{1}}×\frac{\mathrm{1}−\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} }\left(−\mathrm{1}\right) \\ $$$$\mathrm{L}=−\mathrm{1}×\mathrm{1}×\mathrm{1}×\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
