Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 145531 by mathdanisur last updated on 05/Jul/21

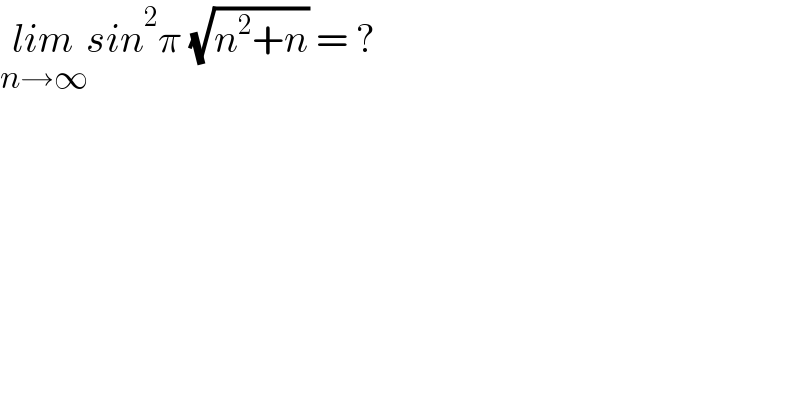
lim_(n→∞) sin^2 π (√(n^2 +n)) = ?

$$\underset{{n}\rightarrow\infty} {{lim}sin}^{\mathrm{2}} \pi\:\sqrt{{n}^{\mathrm{2}} +{n}}\:=\:? \\ $$

Answered by Olaf_Thorendsen last updated on 05/Jul/21

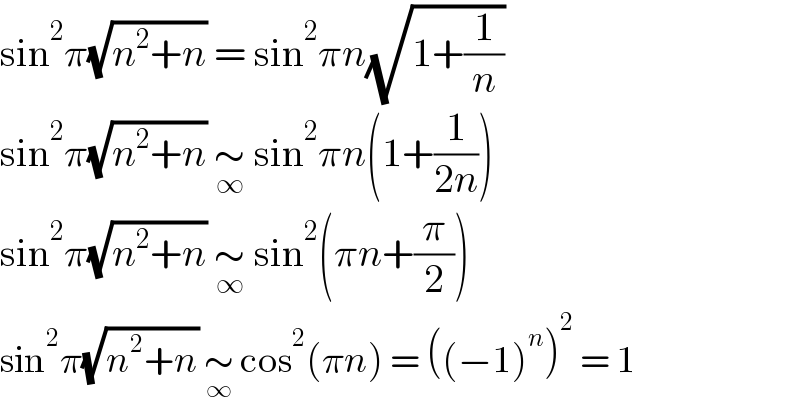
sin^2 π(√(n^2 +n)) = sin^2 πn(√(1+(1/n))) sin^2 π(√(n^2 +n)) ∼_∞ sin^2 πn(1+(1/(2n))) sin^2 π(√(n^2 +n)) ∼_∞ sin^2 (πn+(π/2)) sin^2 π(√(n^2 +n)) ∼_∞ cos^2 (πn) = ((−1)^n )^2 = 1

$$\mathrm{sin}^{\mathrm{2}} \pi\sqrt{{n}^{\mathrm{2}} +{n}}\:=\:\mathrm{sin}^{\mathrm{2}} \pi{n}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{n}}} \\ $$$$\mathrm{sin}^{\mathrm{2}} \pi\sqrt{{n}^{\mathrm{2}} +{n}}\:\underset{\infty} {\sim}\:\mathrm{sin}^{\mathrm{2}} \pi{n}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right) \\ $$$$\mathrm{sin}^{\mathrm{2}} \pi\sqrt{{n}^{\mathrm{2}} +{n}}\:\underset{\infty} {\sim}\:\mathrm{sin}^{\mathrm{2}} \left(\pi{n}+\frac{\pi}{\mathrm{2}}\right) \\ $$$$\mathrm{sin}^{\mathrm{2}} \pi\sqrt{{n}^{\mathrm{2}} +{n}}\:\underset{\infty} {\sim}\:\mathrm{cos}^{\mathrm{2}} \left(\pi{n}\right)\:=\:\left(\left(−\mathrm{1}\right)^{{n}} \right)^{\mathrm{2}} \:=\:\mathrm{1} \\ $$

Commented by mathdanisur last updated on 05/Jul/21

cool thanks Ser

$${cool}\:{thanks}\:{Ser} \\ $$

Commented by mathdanisur last updated on 06/Jul/21

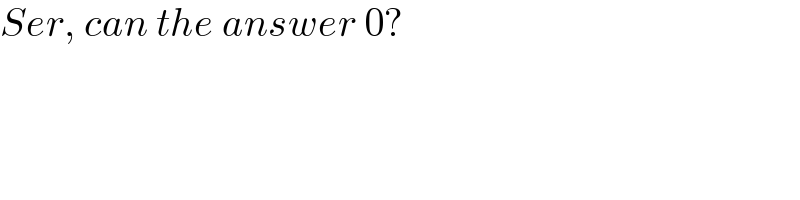
Ser, can the answer 0?

$${Ser},\:{can}\:{the}\:{answer}\:\mathrm{0}? \\ $$

Answered by mathmax by abdo last updated on 05/Jul/21

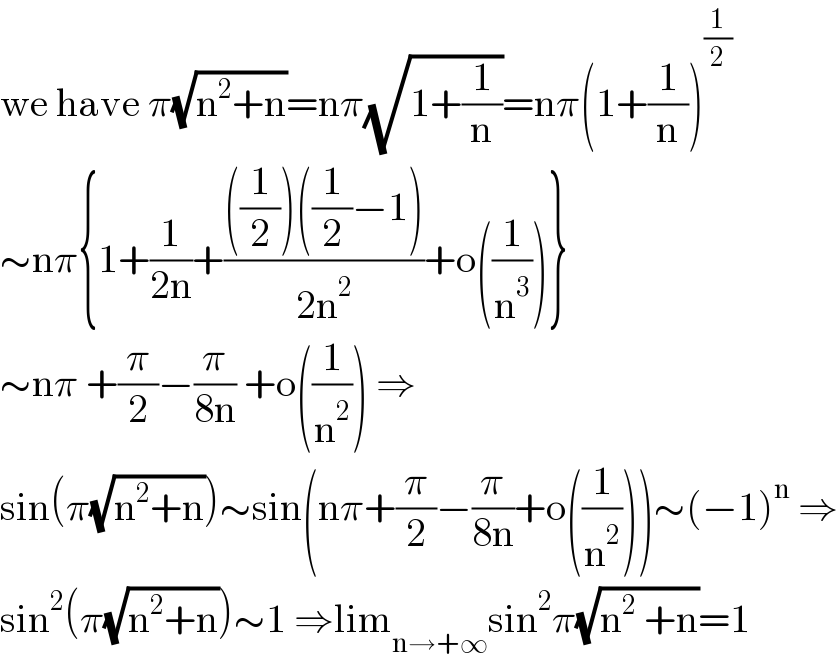
we have π(√(n^2 +n))=nπ(√(1+(1/n)))=nπ(1+(1/n))^(1/2) ∼nπ{1+(1/(2n))+((((1/2))((1/2)−1))/(2n^2 ))+o((1/n^3 ))} ∼nπ +(π/2)−(π/(8n)) +o((1/n^2 )) ⇒ sin(π(√(n^2 +n)))∼sin(nπ+(π/2)−(π/(8n))+o((1/n^2 )))∼(−1)^n ⇒ sin^2 (π(√(n^2 +n)))∼1 ⇒lim_(n→+∞) sin^2 π(√(n^2 +n))=1

$$\mathrm{we}\:\mathrm{have}\:\pi\sqrt{\mathrm{n}^{\mathrm{2}} +\mathrm{n}}=\mathrm{n}\pi\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}}=\mathrm{n}\pi\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\sim\mathrm{n}\pi\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}}+\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2n}^{\mathrm{2}} }+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\right)\right\} \\ $$$$\sim\mathrm{n}\pi\:+\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{8n}}\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$$\mathrm{sin}\left(\pi\sqrt{\mathrm{n}^{\mathrm{2}} +\mathrm{n}}\right)\sim\mathrm{sin}\left(\mathrm{n}\pi+\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{8n}}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)\right)\sim\left(−\mathrm{1}\right)^{\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{sin}^{\mathrm{2}} \left(\pi\sqrt{\mathrm{n}^{\mathrm{2}} +\mathrm{n}}\right)\sim\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{sin}^{\mathrm{2}} \pi\sqrt{\mathrm{n}^{\mathrm{2}} \:+\mathrm{n}}=\mathrm{1} \\ $$

Commented by mathdanisur last updated on 05/Jul/21

cool thanks Ser

$${cool}\:{thanks}\:{Ser} \\ $$

Commented by mathdanisur last updated on 06/Jul/21

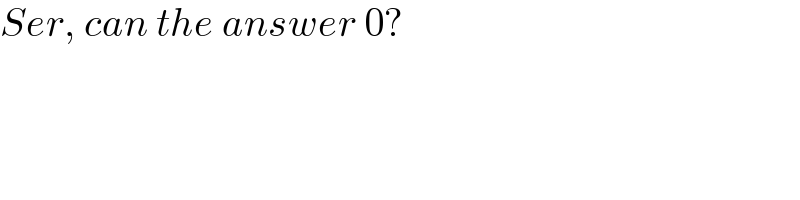
Ser, can the answer 0?

$${Ser},\:{can}\:{the}\:{answer}\:\mathrm{0}? \\ $$

Answered by Dwaipayan Shikari last updated on 05/Jul/21

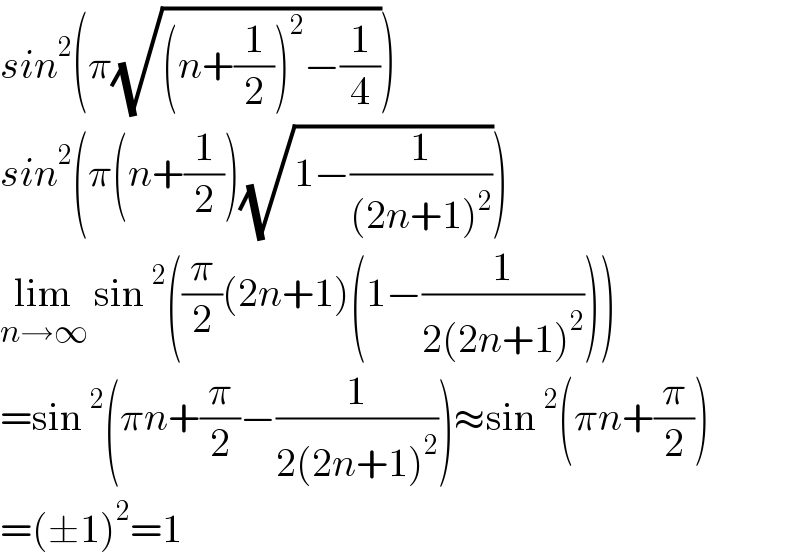
sin^2 (π(√((n+(1/2))^2 −(1/4)))) sin^2 (π(n+(1/2))(√(1−(1/((2n+1)^2 ))))) lim_(n→∞) sin^2 ((π/2)(2n+1)(1−(1/(2(2n+1)^2 )))) =sin^2 (πn+(π/2)−(1/(2(2n+1)^2 )))≈sin^2 (πn+(π/2)) =(±1)^2 =1

$${sin}^{\mathrm{2}} \left(\pi\sqrt{\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}\right) \\ $$$${sin}^{\mathrm{2}} \left(\pi\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }}\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\right)\right) \\ $$$$=\mathrm{sin}\:^{\mathrm{2}} \left(\pi{n}+\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\right)\approx\mathrm{sin}\:^{\mathrm{2}} \left(\pi{n}+\frac{\pi}{\mathrm{2}}\right) \\ $$$$=\left(\pm\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$

Commented by mathdanisur last updated on 05/Jul/21

cool thanks Ser

$${cool}\:{thanks}\:{Ser} \\ $$

Commented by mathdanisur last updated on 06/Jul/21

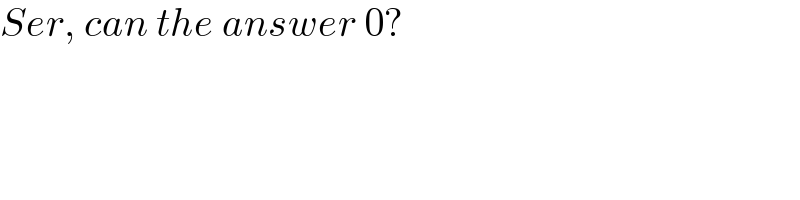
Ser, can the answer 0?

$${Ser},\:{can}\:{the}\:{answer}\:\mathrm{0}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com