
Question Number 204574 by universe last updated on 22/Feb/24
![lim_(n→∞) n^(−3/2) [(n+1)^((n+1)) (n+2)^((n+2)) ...(2n)^(2n) ]^(1/n^2 ) = ?](Q204574.png)
$$ \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{n}^{−\mathrm{3}/\mathrm{2}} \left[\left(\mathrm{n}+\mathrm{1}\right)^{\left(\mathrm{n}+\mathrm{1}\right)} \left(\mathrm{n}+\mathrm{2}\right)^{\left(\mathrm{n}+\mathrm{2}\right)} ...\left(\mathrm{2n}\right)^{\mathrm{2n}} \right]^{\mathrm{1}/\mathrm{n}^{\mathrm{2}} } \:=\:? \\ $$$$ \\ $$
Answered by TonyCWX08 last updated on 22/Feb/24

$${know} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{n}^{{a}} }\right)=\mathrm{0},\:{a}=\:{Positive}\:{Number} \\ $$$$ \\ $$$${n}^{−\frac{\mathrm{3}}{\mathrm{2}}} =\frac{\mathrm{1}}{{n}^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{n}^{\frac{\mathrm{3}}{\mathrm{2}}} }\right) \\ $$$$=\mathrm{0} \\ $$$$ \\ $$$${Anything}\:{Multiply}\:\mathrm{0}\:{is}\:\mathrm{0} \\ $$$${Final}\:{answer}=\mathrm{0} \\ $$
Commented by mr W last updated on 22/Feb/24
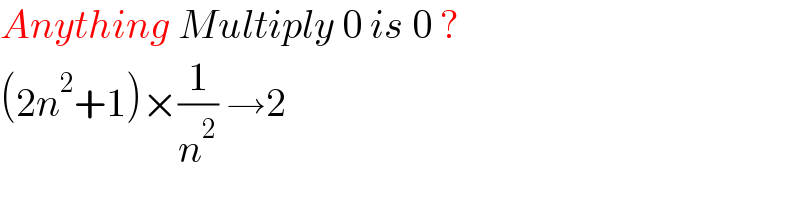
$${Anything}\:{Multiply}\:\mathrm{0}\:{is}\:\mathrm{0}\:? \\ $$$$\left(\mathrm{2}{n}^{\mathrm{2}} +\mathrm{1}\right)×\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\rightarrow\mathrm{2} \\ $$
Commented by TonyCWX08 last updated on 22/Feb/24
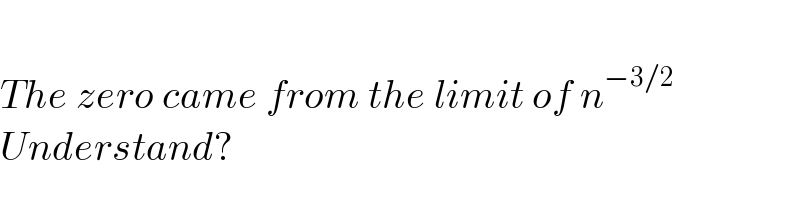
$$ \\ $$$${The}\:{zero}\:{came}\:{from}\:{the}\:{limit}\:{of}\:{n}^{−\mathrm{3}/\mathrm{2}} \\ $$$${Understand}? \\ $$
Commented by mr W last updated on 22/Feb/24
![i just wanted to give an example that ∞×0≠0. so it is not enough only to know n^(−(3/2)) →0 and then say the final limit is zero. what is about [(n+1)^((n+1)) ....(2n)^(2n) ]^(1/n^2 ) ?](Q204579.png)
$${i}\:{just}\:{wanted}\:{to}\:{give}\:{an}\:{example} \\ $$$${that}\:\infty×\mathrm{0}\neq\mathrm{0}.\:{so}\:{it}\:{is}\:{not}\:{enough}\:{only} \\ $$$${to}\:{know}\:\:{n}^{−\frac{\mathrm{3}}{\mathrm{2}}} \rightarrow\mathrm{0}\:{and}\:{then}\:{say}\:{the} \\ $$$${final}\:{limit}\:{is}\:{zero}.\:{what}\:{is}\:{about} \\ $$$$\left[\left({n}+\mathrm{1}\right)^{\left({n}+\mathrm{1}\right)} ....\left(\mathrm{2}{n}\right)^{\mathrm{2}{n}} \right]^{\frac{\mathrm{1}}{{n}^{\mathrm{2}} }} \:? \\ $$
Answered by witcher3 last updated on 22/Feb/24
![Ω=(1/(n(√n)))e^((1/n^2 )[Σ_(k=1) ^n (n+k)ln(n+k)]) =(1/(n(√n)))e^((1/n)(Σ_(k=1) ^n (1+(k/n))(ln(n)+ln(1+(k/n)))) =(e^((1/n)Σ_(k=1) ^n (1+(k/n))ln(n)+(1/n)Σ_(k=1) ^n (1+(k/n))ln(1+(k/n))) /(n(√n))) =((ln(n))/n)Σ_(k=1) ^n (1+(k/n))=((ln(n))/n)(n+((n+1)/2))..S_1 lim_(n→0) (1/n)Σ_1 ^n (1+(k/n))ln(1+(k/n))=^(Riemann Sum) ∫_0 ^1 (1+x)ln(1+x)dx ∫_0 ^1 (1+x)ln(1+x)dx=[(((1+x)^2 )/2)ln(1+x)]_0 ^1 −∫_0 ^1 ((1+x)/2)dx=2ln(2)−(3/2) ⇒∀ε>0 ∃N∈N;∀n≥N;2ln(2)−(3/2)−ε≤S_2 =(1/n)Σ_(k=1) ^n (1+(k/n))ln(1+(k/n))≤2ln(2)−(3/2)+ε... Ω=(1/(n(√n)))e^((1/n)(((3n+1)/2))ln(n)+S_2 ) =(e^((3/2)ln(n)+((ln(n))/(2n))+S_2 ) /(n(√n)))=(n^(3/2) /n^(3/2) ).e^(((ln(n))/(2n))+S_2 ) =e^(((ln(n))/(2n))+S_2 ) ;((ln(n))/(2n))→0;S_2 →2ln(2)−(3/2) lim_(n→∞) Ω=e^(2ln(2)−(3/2)) =(4/(e(√e)))](Q204589.png)
$$\Omega=\frac{\mathrm{1}}{\mathrm{n}\sqrt{\mathrm{n}}}\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\left[\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{n}+\mathrm{k}\right)\mathrm{ln}\left(\mathrm{n}+\mathrm{k}\right)\right]} =\frac{\mathrm{1}}{\mathrm{n}\sqrt{\mathrm{n}}}\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{n}}\left(\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\left(\mathrm{ln}\left(\mathrm{n}\right)+\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\right)\right.} \\ $$$$=\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\mathrm{ln}\left(\mathrm{n}\right)+\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)} }{\mathrm{n}\sqrt{\mathrm{n}}} \\ $$$$=\frac{\mathrm{ln}\left(\mathrm{n}\right)}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)=\frac{\mathrm{ln}\left(\mathrm{n}\right)}{\mathrm{n}}\left(\mathrm{n}+\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}\right)..\mathrm{S}_{\mathrm{1}} \\ $$$$\underset{\mathrm{n}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\overset{\mathrm{Riemann}\:\mathrm{Sum}} {=}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{dx}=\left[\frac{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}+\mathrm{x}}{\mathrm{2}}\mathrm{dx}=\mathrm{2ln}\left(\mathrm{2}\right)−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\forall\epsilon>\mathrm{0}\:\exists\mathrm{N}\in\mathbb{N};\forall\mathrm{n}\geqslant\mathbb{N};\mathrm{2ln}\left(\mathrm{2}\right)−\frac{\mathrm{3}}{\mathrm{2}}−\epsilon\leqslant\mathrm{S}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\leqslant\mathrm{2ln}\left(\mathrm{2}\right)−\frac{\mathrm{3}}{\mathrm{2}}+\epsilon... \\ $$$$ \\ $$$$\Omega=\frac{\mathrm{1}}{\mathrm{n}\sqrt{\mathrm{n}}}\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{n}}\left(\frac{\mathrm{3n}+\mathrm{1}}{\mathrm{2}}\right)\mathrm{ln}\left(\mathrm{n}\right)+\mathrm{S}_{\mathrm{2}} } =\frac{\mathrm{e}^{\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{n}\right)+\frac{\mathrm{ln}\left(\mathrm{n}\right)}{\mathrm{2n}}+\mathrm{S}_{\mathrm{2}} } }{\mathrm{n}\sqrt{\mathrm{n}}}=\frac{\mathrm{n}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{n}^{\frac{\mathrm{3}}{\mathrm{2}}} }.\mathrm{e}^{\frac{\mathrm{ln}\left(\mathrm{n}\right)}{\mathrm{2n}}+\mathrm{S}_{\mathrm{2}} } \\ $$$$=\mathrm{e}^{\frac{\mathrm{ln}\left(\mathrm{n}\right)}{\mathrm{2n}}+\mathrm{S}_{\mathrm{2}} } ;\frac{\mathrm{ln}\left(\mathrm{n}\right)}{\mathrm{2n}}\rightarrow\mathrm{0};\mathrm{S}_{\mathrm{2}} \rightarrow\mathrm{2ln}\left(\mathrm{2}\right)−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\Omega=\mathrm{e}^{\mathrm{2ln}\left(\mathrm{2}\right)−\frac{\mathrm{3}}{\mathrm{2}}} =\frac{\mathrm{4}}{\mathrm{e}\sqrt{\mathrm{e}}} \\ $$$$ \\ $$
Commented by universe last updated on 22/Feb/24
$${thank}\:{u}\:{so}\:{much}\:{sir} \\ $$
Commented by universe last updated on 22/Feb/24
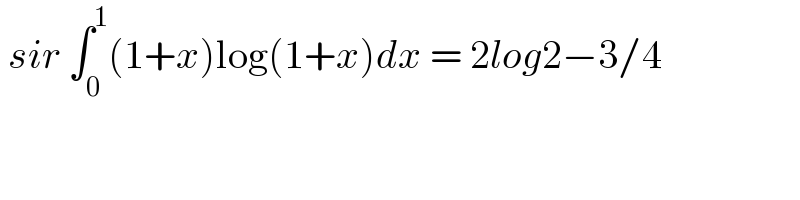
$$\:{sir}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{x}\right)\mathrm{log}\left(\mathrm{1}+{x}\right){dx}\:=\:\mathrm{2}{log}\mathrm{2}−\mathrm{3}/\mathrm{4}\: \\ $$
Commented by witcher3 last updated on 22/Feb/24

$$\mathrm{yes}\:\mathrm{sorry}\:\mathrm{for}\:\mathrm{the}\:\mathrm{mistack}\:\mathrm{Too}\:\mathrm{busy} \\ $$
Commented by universe last updated on 23/Feb/24
$${no}\:{problem}\:{sir}\:{your}\:{approch}\:{is}\:{right} \\ $$
