
Question Number 182659 by mathlove last updated on 12/Dec/22
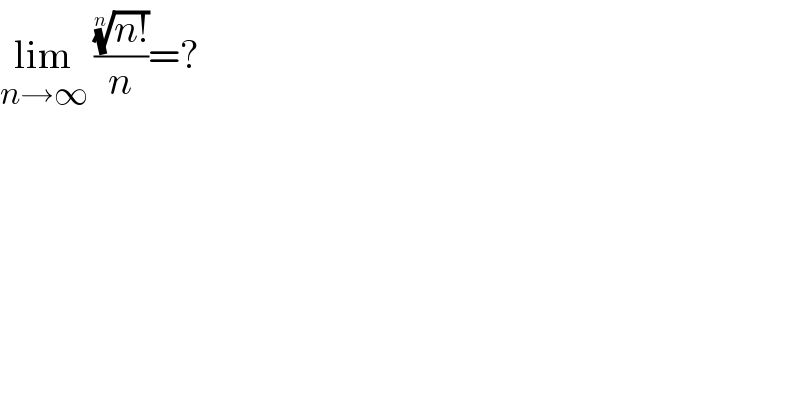
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt[{{n}}]{{n}!}}{{n}}=? \\ $$
Answered by Frix last updated on 12/Dec/22
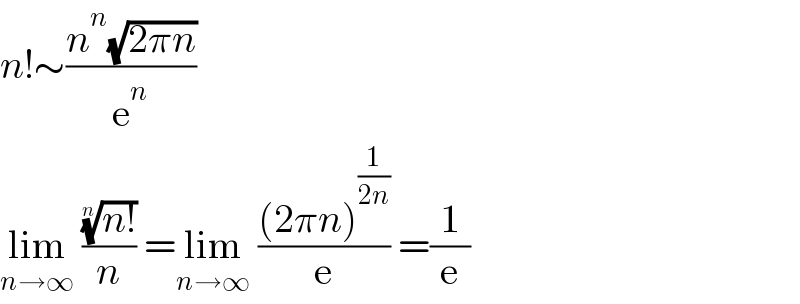
$${n}!\sim\frac{{n}^{{n}} \sqrt{\mathrm{2}\pi{n}}}{\mathrm{e}^{{n}} } \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt[{{n}}]{{n}!}}{{n}}\:=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left(\mathrm{2}\pi{n}\right)^{\frac{\mathrm{1}}{\mathrm{2}{n}}} }{\mathrm{e}}\:=\frac{\mathrm{1}}{\mathrm{e}} \\ $$
