
Question Number 101822 by john santu last updated on 04/Jul/20
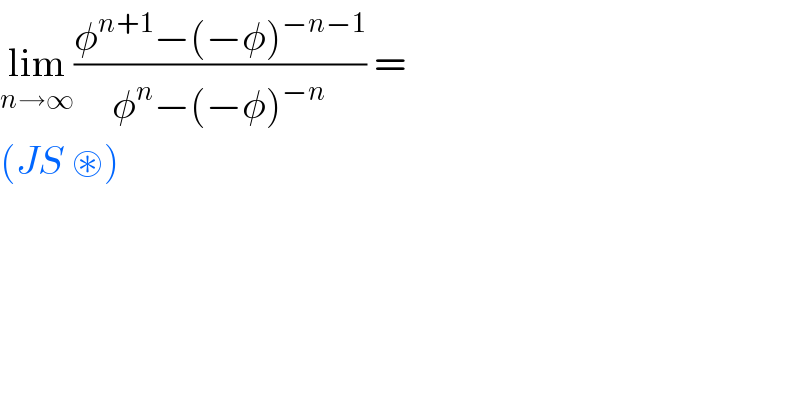
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\phi^{{n}+\mathrm{1}} −\left(−\phi\right)^{−{n}−\mathrm{1}} }{\phi^{{n}} −\left(−\phi\right)^{−{n}} }\:=\: \\ $$$$\left({JS}\:\circledast\right) \\ $$
Answered by bobhans last updated on 05/Jul/20
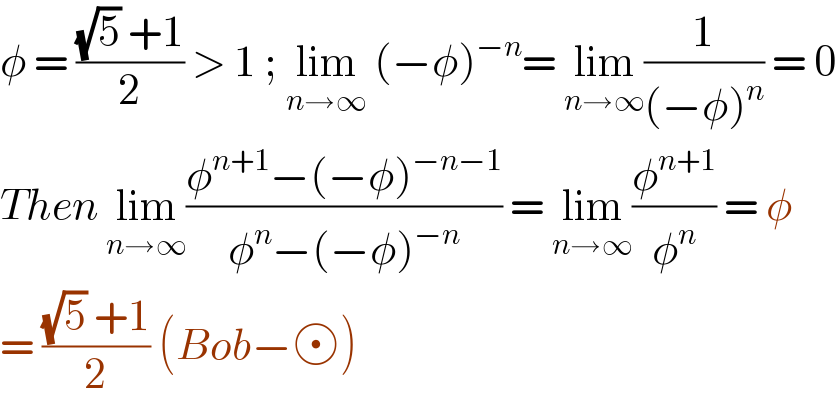
$$\phi\:=\:\frac{\sqrt{\mathrm{5}}\:+\mathrm{1}}{\mathrm{2}}\:>\:\mathrm{1}\:;\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(−\phi\right)^{−{n}} =\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\left(−\phi\right)^{{n}} }\:=\:\mathrm{0} \\ $$$${Then}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\phi^{{n}+\mathrm{1}} −\left(−\phi\right)^{−{n}−\mathrm{1}} }{\phi^{{n}} −\left(−\phi\right)^{−{n}} }\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\phi^{{n}+\mathrm{1}} }{\phi^{{n}} }\:=\:\phi \\ $$$$=\:\frac{\sqrt{\mathrm{5}}\:+\mathrm{1}}{\mathrm{2}}\:\left({Bob}− \right) \\ $$
