
Question Number 167332 by Amazigh last updated on 13/Mar/22
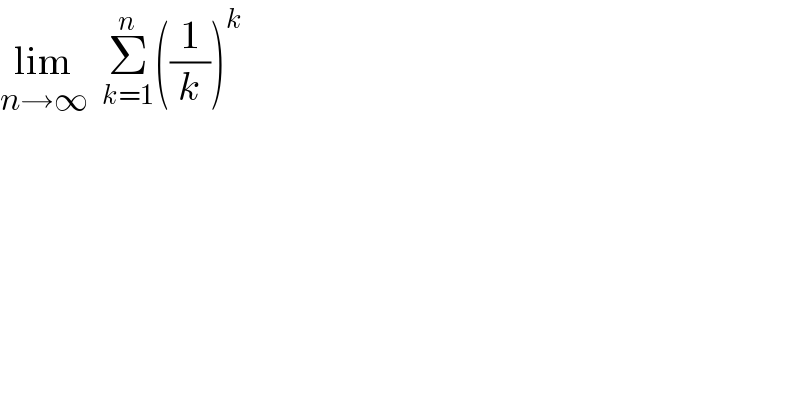
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{k}}\right)^{{k}} \\ $$
Answered by LEKOUMA last updated on 14/Mar/22
![S_n =lim_(n→0) Σ_(k=1) ^n ((1/k))^k On prend, a=0 et b=1 Choisison f(x)=x^k f est continue sur [0,1] S_n → ∫_0 ^1 f(x)dx=∫_0 ^1 x^k dx ∫_0 ^1 x^k dx=[(x^(k+1) /(k+1))]_0 ^1 =(1/(k+1)) lim_(n→∞) Σ_(k=1) ^n ((1/k))^k =(1/(k+1))](Q167363.png)
$${S}_{{n}} =\underset{{n}\rightarrow\mathrm{0}} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{k}}\right)^{{k}} \\ $$$${On}\:{prend},\:\:{a}=\mathrm{0}\:{et}\:{b}=\mathrm{1}\: \\ $$$${Choisison}\:{f}\left({x}\right)={x}^{{k}} \\ $$$${f}\:{est}\:{continue}\:{sur}\:\left[\mathrm{0},\mathrm{1}\right]\: \\ $$$${S}_{{n}} \rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{k}} {dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{k}} {dx}=\left[\frac{{x}^{{k}+\mathrm{1}} }{{k}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{{k}+\mathrm{1}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{k}}\right)^{{k}} =\frac{\mathrm{1}}{{k}+\mathrm{1}} \\ $$
Commented by Amazigh last updated on 17/Mar/22
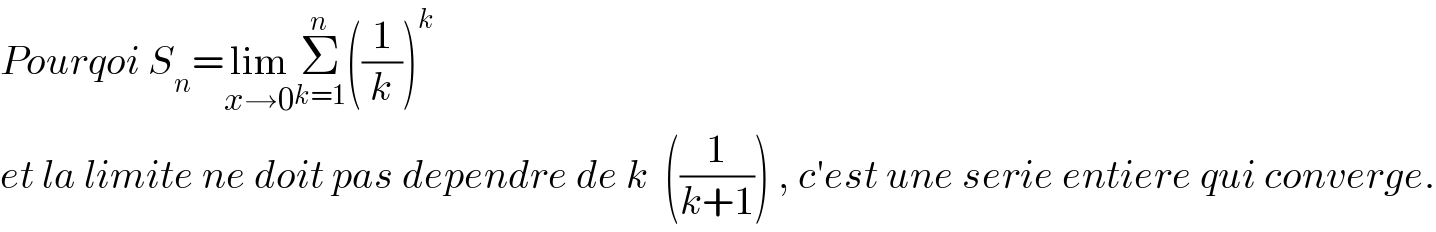
$${Pourqoi}\:{S}_{{n}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{k}}\right)^{{k}} \\ $$$${et}\:{la}\:{limite}\:{ne}\:{doit}\:{pas}\:{dependre}\:{de}\:{k}\:\:\left(\frac{\mathrm{1}}{{k}+\mathrm{1}}\right)\:,\:{c}'{est}\:{une}\:{serie}\:{entiere}\:{qui}\:{converge}. \\ $$
