Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 115575 by Aziztisffola last updated on 26/Sep/20

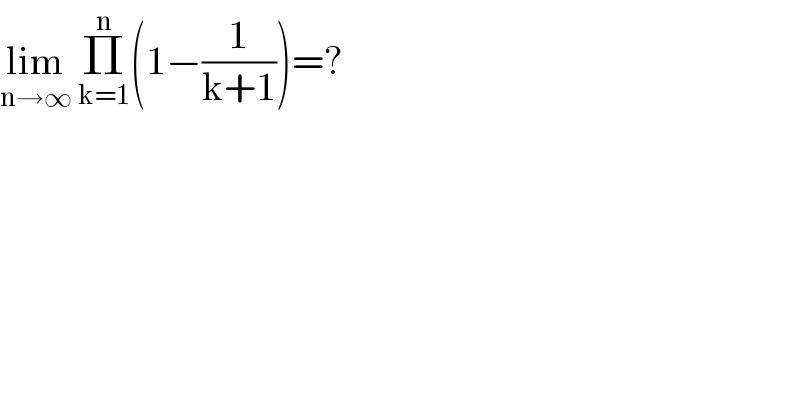
lim_(n→∞) Π_(k=1) ^n (1−(1/(k+1)))=?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\right)=? \\ $$

Commented by Dwaipayan Shikari last updated on 26/Sep/20

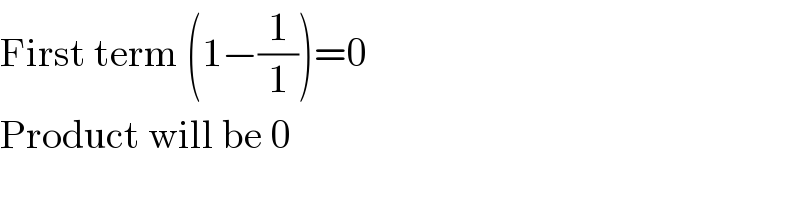
First term (1−(1/1))=0 Product will be 0

$$\mathrm{First}\:\mathrm{term}\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}}\right)=\mathrm{0} \\ $$$$\mathrm{Product}\:\mathrm{will}\:\mathrm{be}\:\mathrm{0} \\ $$

Commented by Aziztisffola last updated on 26/Sep/20

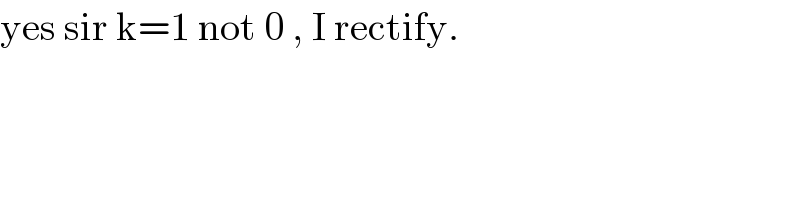
yes sir k=1 not 0 , I rectify.

$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{k}=\mathrm{1}\:\mathrm{not}\:\mathrm{0}\:,\:\mathrm{I}\:\mathrm{rectify}. \\ $$

Answered by TANMAY PANACEA last updated on 26/Sep/20

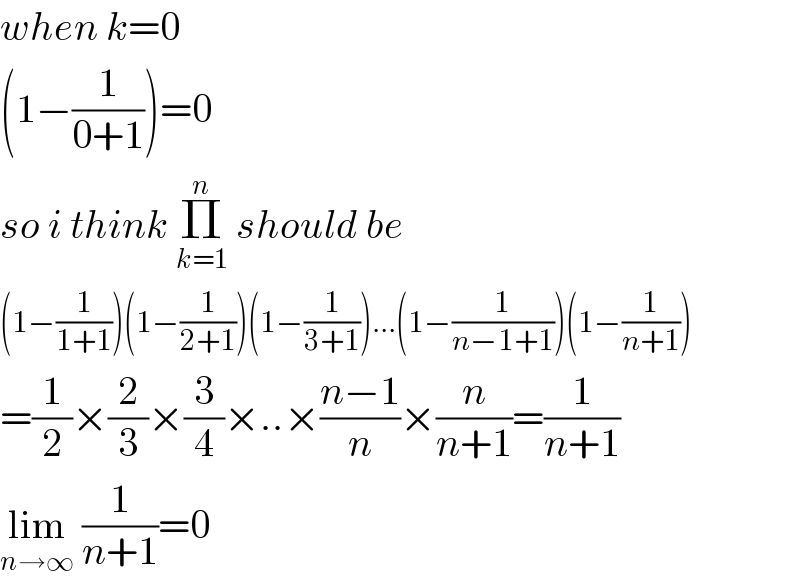
when k=0 (1−(1/(0+1)))=0 so i think Π_(k=1) ^n should be (1−(1/(1+1)))(1−(1/(2+1)))(1−(1/(3+1)))...(1−(1/(n−1+1)))(1−(1/(n+1))) =(1/2)×(2/3)×(3/4)×..×((n−1)/n)×(n/(n+1))=(1/(n+1)) lim_(n→∞) (1/(n+1))=0

$${when}\:{k}=\mathrm{0} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{0}+\mathrm{1}}\right)=\mathrm{0} \\ $$$${so}\:{i}\:{think}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\:{should}\:{be} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}+\mathrm{1}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}+\mathrm{1}}\right)...\left(\mathrm{1}−\frac{\mathrm{1}}{{n}−\mathrm{1}+\mathrm{1}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{4}}×..×\frac{{n}−\mathrm{1}}{{n}}×\frac{{n}}{{n}+\mathrm{1}}=\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{n}+\mathrm{1}}=\mathrm{0} \\ $$

Commented by Aziztisffola last updated on 26/Sep/20

yes sir k=1.

$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{k}=\mathrm{1}. \\ $$

Answered by Dwaipayan Shikari last updated on 26/Sep/20

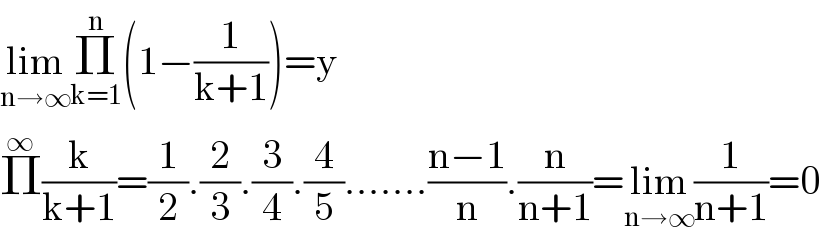
lim_(n→∞) Π_(k=1) ^n (1−(1/(k+1)))=y Π^∞ (k/(k+1))=(1/2).(2/3).(3/4).(4/5).......((n−1)/n).(n/(n+1))=lim_(n→∞) (1/(n+1))=0

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\right)=\mathrm{y} \\ $$$$\overset{\infty} {\prod}\frac{\mathrm{k}}{\mathrm{k}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{3}}{\mathrm{4}}.\frac{\mathrm{4}}{\mathrm{5}}.......\frac{\mathrm{n}−\mathrm{1}}{\mathrm{n}}.\frac{\mathrm{n}}{\mathrm{n}+\mathrm{1}}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}=\mathrm{0} \\ $$

Commented by TANMAY PANACEA last updated on 26/Sep/20

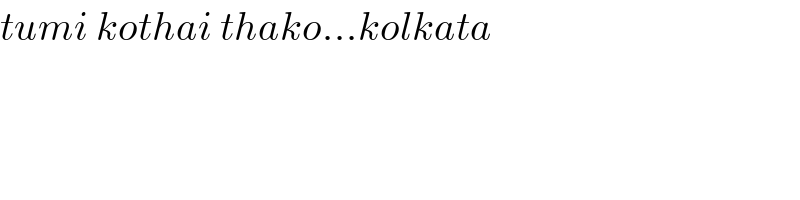
tumi kothai thako...kolkata

$${tumi}\:{kothai}\:{thako}...{kolkata} \\ $$

Commented by Dwaipayan Shikari last updated on 26/Sep/20

Ha sir

$$\mathrm{Ha}\:\mathrm{sir} \\ $$

Commented by TANMAY PANACEA last updated on 26/Sep/20

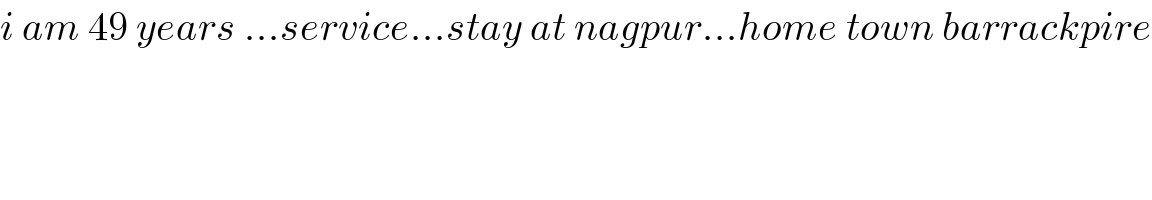
i am 49 years ...service...stay at nagpur...home town barrackpire

$${i}\:{am}\:\mathrm{49}\:{years}\:...{service}...{stay}\:{at}\:{nagpur}...{home}\:{town}\:{barrackpire} \\ $$

Commented by Aziztisffola last updated on 26/Sep/20

That′s it.

$$\mathrm{That}'\mathrm{s}\:\mathrm{it}. \\ $$

Answered by Bird last updated on 27/Sep/20

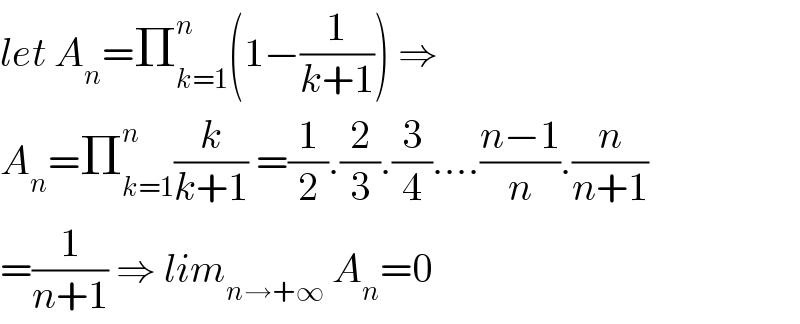
let A_n =Π_(k=1) ^n (1−(1/(k+1))) ⇒ A_n =Π_(k=1) ^n (k/(k+1)) =(1/2).(2/3).(3/4)....((n−1)/n).(n/(n+1)) =(1/(n+1)) ⇒ lim_(n→+∞) A_n =0

$${let}\:{A}_{{n}} =\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{1}−\frac{\mathrm{1}}{{k}+\mathrm{1}}\right)\:\Rightarrow \\ $$$${A}_{{n}} =\prod_{{k}=\mathrm{1}} ^{{n}} \frac{{k}}{{k}+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{3}}{\mathrm{4}}....\frac{{n}−\mathrm{1}}{{n}}.\frac{{n}}{{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\Rightarrow\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com