Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 132321 by Raxreedoroid last updated on 13/Feb/21

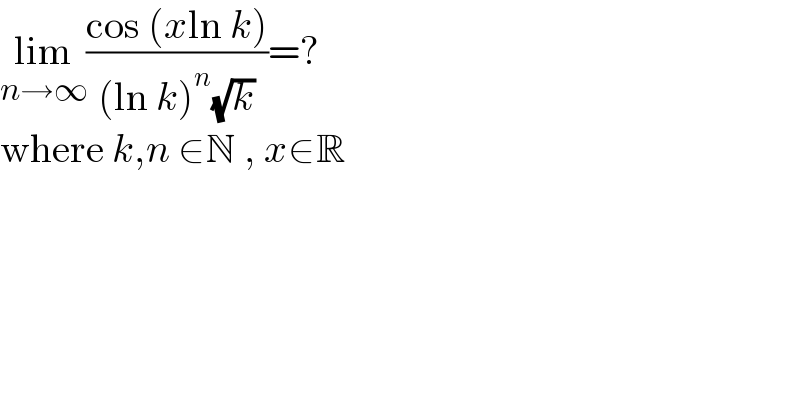
lim_(n→∞) ((cos (xln k))/((ln k)^n (√k)))=? where k,n ∈N , x∈R

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{cos}\:\left({x}\mathrm{ln}\:{k}\right)}{\left(\mathrm{ln}\:{k}\right)^{{n}} \sqrt{{k}}}=? \\ $$$$\mathrm{where}\:{k},{n}\:\in\mathbb{N}\:,\:{x}\in\mathbb{R} \\ $$

Answered by Dwaipayan Shikari last updated on 13/Feb/21

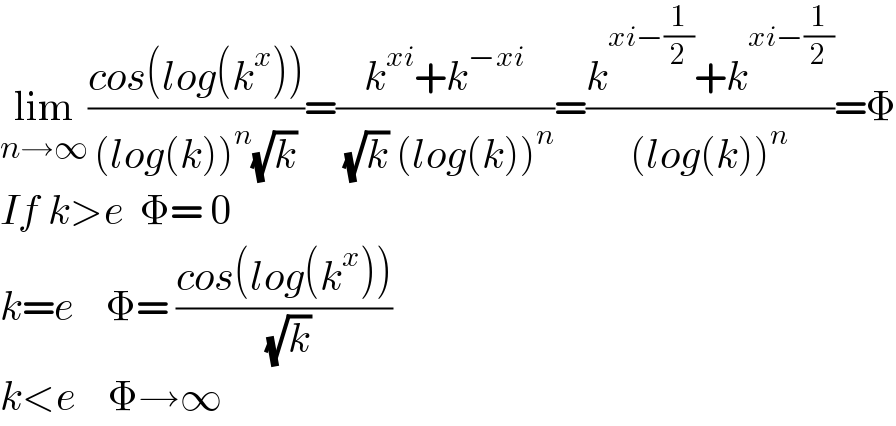
lim_(n→∞) ((cos(log(k^x )))/((log(k))^n (√k)))=((k^(xi) +k^(−xi) )/( (√k) (log(k))^n ))=((k^(xi−(1/2)) +k^(xi−(1/2)) )/((log(k))^n ))=Φ If k>e Φ= 0 k=e Φ= ((cos(log(k^x )))/( (√k))) k<e Φ→∞

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{cos}\left({log}\left({k}^{{x}} \right)\right)}{\left({log}\left({k}\right)\right)^{{n}} \sqrt{{k}}}=\frac{{k}^{{xi}} +{k}^{−{xi}} }{\:\sqrt{{k}}\:\left({log}\left({k}\right)\right)^{{n}} }=\frac{{k}^{{xi}−\frac{\mathrm{1}}{\mathrm{2}}} +{k}^{{xi}−\frac{\mathrm{1}}{\mathrm{2}}} }{\left({log}\left({k}\right)\right)^{{n}} }=\Phi \\ $$$${If}\:{k}>{e}\:\:\Phi=\:\mathrm{0} \\ $$$${k}={e}\:\:\:\:\Phi=\:\frac{{cos}\left({log}\left({k}^{{x}} \right)\right)}{\:\sqrt{{k}}} \\ $$$${k}<{e}\:\:\:\:\Phi\rightarrow\infty \\ $$

Commented by Raxreedoroid last updated on 13/Feb/21

sir I think the answer is always 0 except for k = 1 since cos(x) where x ∈ R is between [−1,1] and lim_(x→∞) (1/(a∙b^x ))=0 so in that case lim_(n→∞) ((cos (log(k^x )))/((log(k))^n (√k)))=(([−1,1])/(incredibly large))=0 ,k≠1

$$\mathrm{sir}\:\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{always}\:\mathrm{0}\:\mathrm{except}\:\mathrm{for}\:\mathrm{k}\:=\:\mathrm{1} \\ $$$$\mathrm{since}\:\mathrm{cos}\left({x}\right)\:\mathrm{where}\:{x}\:\in\:\mathbb{R}\:\mathrm{is}\:\mathrm{between}\:\left[−\mathrm{1},\mathrm{1}\right] \\ $$$$\mathrm{and}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{a}\centerdot{b}^{{x}} }=\mathrm{0} \\ $$$$\mathrm{so}\:\mathrm{in}\:\mathrm{that}\:\mathrm{case} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{cos}\:\left(\mathrm{log}\left(\mathrm{k}^{\mathrm{x}} \right)\right)}{\left(\mathrm{log}\left(\mathrm{k}\right)\right)^{\mathrm{n}} \:\sqrt{{k}}}=\frac{\left[−\mathrm{1},\mathrm{1}\right]}{\mathrm{incredibly}\:\mathrm{large}}=\mathrm{0}\:,{k}\neq\mathrm{1} \\ $$

Commented by Raxreedoroid last updated on 13/Feb/21

sorry my mistake ln(k) where k>1 is between (0,∞) so your answer was right

$$\mathrm{sorry}\:\mathrm{my}\:\mathrm{mistake} \\ $$$$\mathrm{ln}\left(\mathrm{k}\right)\:\mathrm{where}\:\mathrm{k}>\mathrm{1}\:\mathrm{is}\:\mathrm{between}\:\left(\mathrm{0},\infty\right) \\ $$$$\mathrm{so}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{was}\:\mathrm{right} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com