
Question Number 69482 by Henri Boucatchou last updated on 24/Sep/19
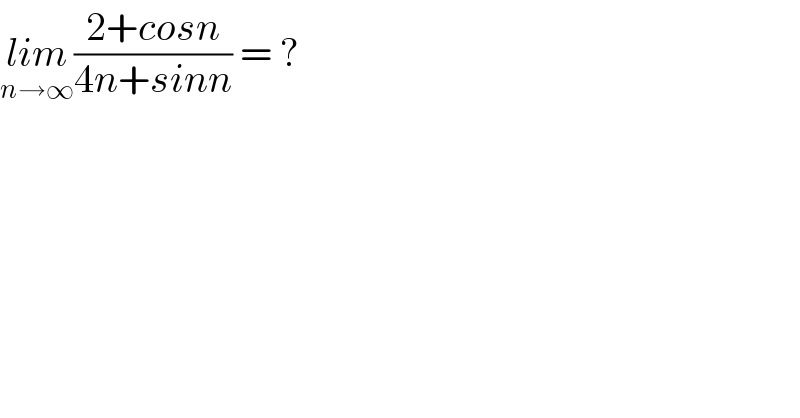
$$\underset{{n}\rightarrow\infty} {{lim}}\frac{\mathrm{2}+{cosn}}{\mathrm{4}{n}+{sinn}}\:=\:? \\ $$
Commented by Tony Lin last updated on 24/Sep/19

$$−\mathrm{1}\leqslant{cosn}\leqslant\mathrm{1} \\ $$$$\mathrm{1}\leqslant\mathrm{2}+{cosn}\leqslant\mathrm{3} \\ $$$$−\mathrm{1}\leqslant{sinn}\leqslant\mathrm{1} \\ $$$$−\mathrm{1}+\mathrm{4}{n}\leqslant\mathrm{4}{n}+{sinn}\leqslant\mathrm{1}+\mathrm{4}{n} \\ $$$$\frac{\mathrm{1}}{−\mathrm{1}+\mathrm{4}{n}}\leqslant\frac{\mathrm{2}+{cosn}}{\mathrm{4}{n}+{sinn}}\leqslant\frac{\mathrm{3}}{\mathrm{1}+\mathrm{4}{n}} \\ $$$$\because\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{−\mathrm{1}+\mathrm{4}{n}}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{3}}{\mathrm{1}+\mathrm{4}{n}}=\mathrm{0} \\ $$$$\therefore{By}\:{Squeeze}\:{Theorem} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}+{cosn}}{\mathrm{4}{n}+{sinn}}=\mathrm{0} \\ $$
Answered by $@ty@m123 last updated on 24/Sep/19
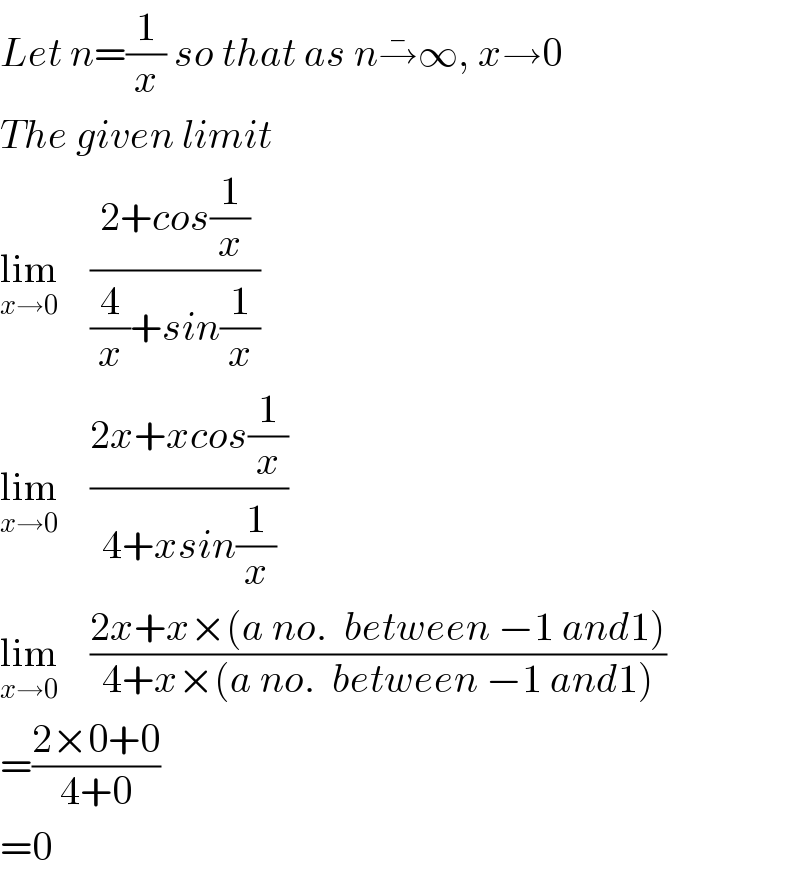
$${Let}\:{n}=\frac{\mathrm{1}}{{x}}\:{so}\:{that}\:{as}\:{n}\bar {\rightarrow}\infty,\:{x}\rightarrow\mathrm{0} \\ $$$${The}\:{given}\:{limit} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{\mathrm{2}+{cos}\frac{\mathrm{1}}{{x}}}{\frac{\mathrm{4}}{{x}}+{sin}\frac{\mathrm{1}}{{x}}}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{\mathrm{2}{x}+{xcos}\frac{\mathrm{1}}{{x}}}{\mathrm{4}+{xsin}\frac{\mathrm{1}}{{x}}}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{\mathrm{2}{x}+{x}×\left({a}\:{no}.\:\:{between}\:−\mathrm{1}\:{and}\mathrm{1}\right)}{\mathrm{4}+{x}×\left({a}\:{no}.\:\:{between}\:−\mathrm{1}\:{and}\mathrm{1}\right)}\: \\ $$$$=\frac{\mathrm{2}×\mathrm{0}+\mathrm{0}}{\mathrm{4}+\mathrm{0}} \\ $$$$=\mathrm{0} \\ $$
