Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 196471 by Tawa11 last updated on 25/Aug/23

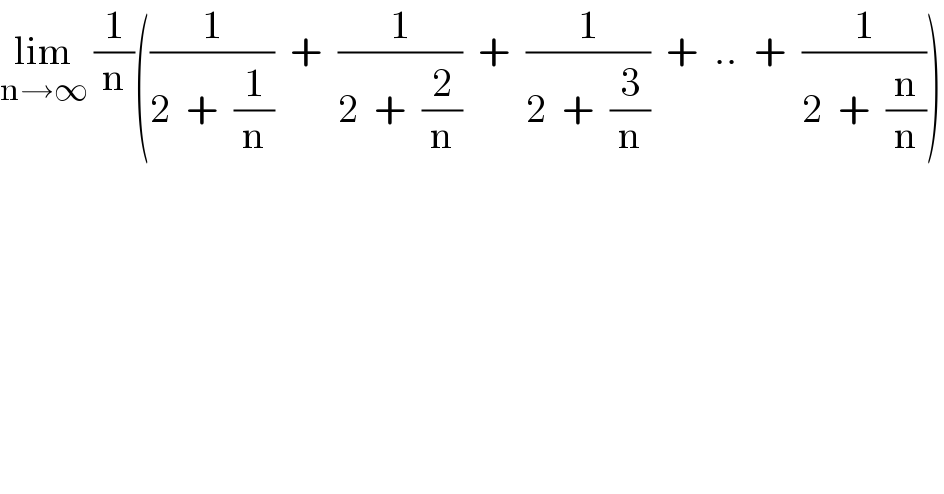
lim_(n→∞) (1/n)((1/(2 + (1/n))) + (1/(2 + (2/n))) + (1/(2 + (3/n))) + .. + (1/(2 + (n/n))))

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{n}}\left(\frac{\mathrm{1}}{\mathrm{2}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{n}}}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{2}\:\:+\:\:\frac{\mathrm{2}}{\mathrm{n}}}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{2}\:\:+\:\:\frac{\mathrm{3}}{\mathrm{n}}}\:\:+\:\:..\:\:+\:\:\frac{\mathrm{1}}{\mathrm{2}\:\:+\:\:\frac{\mathrm{n}}{\mathrm{n}}}\right) \\ $$

Answered by mr W last updated on 25/Aug/23

=∫_0 ^1 (dx/(2+x)) =[ln (2+x)]_0 ^1 =ln 3−ln 2 =ln (3/2)

$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{2}+{x}} \\ $$$$=\left[\mathrm{ln}\:\left(\mathrm{2}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{ln}\:\mathrm{3}−\mathrm{ln}\:\mathrm{2} \\ $$$$=\mathrm{ln}\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Commented by Tawa11 last updated on 25/Aug/23

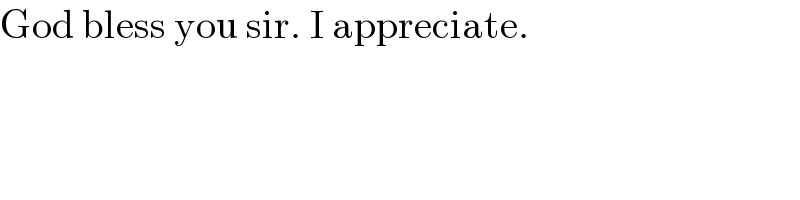
God bless you sir. I appreciate.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by Tawa11 last updated on 25/Aug/23

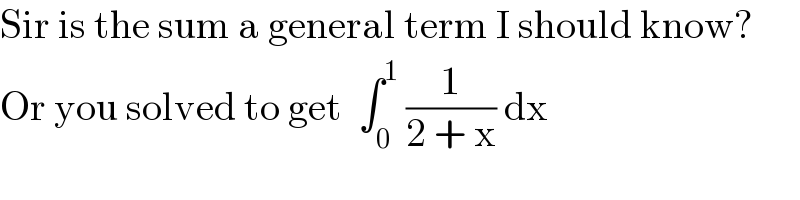
Sir is the sum a general term I should know? Or you solved to get ∫_0 ^1 (1/(2 + x)) dx

$$\mathrm{Sir}\:\mathrm{is}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{a}\:\mathrm{general}\:\mathrm{term}\:\mathrm{I}\:\mathrm{should}\:\mathrm{know}? \\ $$$$\mathrm{Or}\:\mathrm{you}\:\mathrm{solved}\:\mathrm{to}\:\mathrm{get}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{2}\:+\:\mathrm{x}}\:\mathrm{dx} \\ $$

Commented by mr W last updated on 25/Aug/23

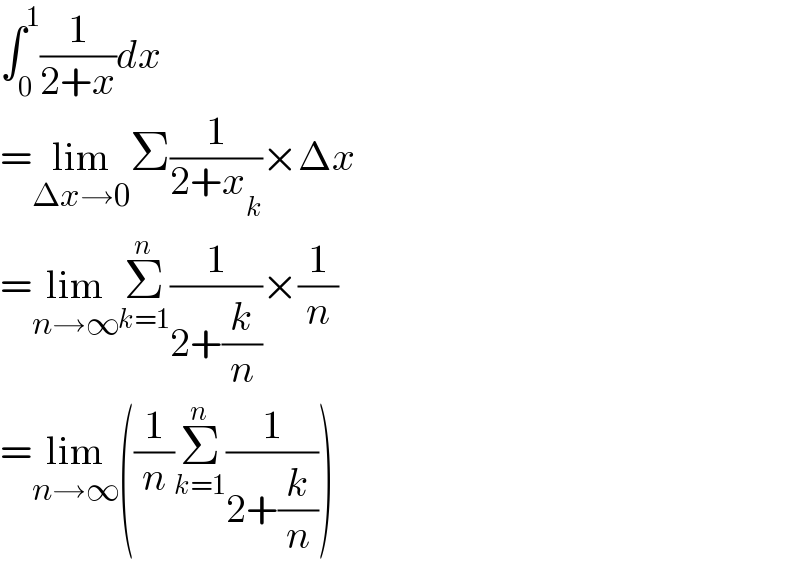
∫_0 ^1 (1/(2+x))dx =lim_(Δx→0) Σ(1/(2+x_k ))×Δx =lim_(n→∞) Σ_(k=1) ^n (1/(2+(k/n)))×(1/n) =lim_(n→∞) ((1/n)Σ_(k=1) ^n (1/(2+(k/n))))

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}+{x}}{dx} \\ $$$$=\underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\Sigma\frac{\mathrm{1}}{\mathrm{2}+{x}_{{k}} }×\Delta{x} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}+\frac{{k}}{{n}}}×\frac{\mathrm{1}}{{n}} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}+\frac{{k}}{{n}}}\right) \\ $$

Commented by mr W last updated on 25/Aug/23

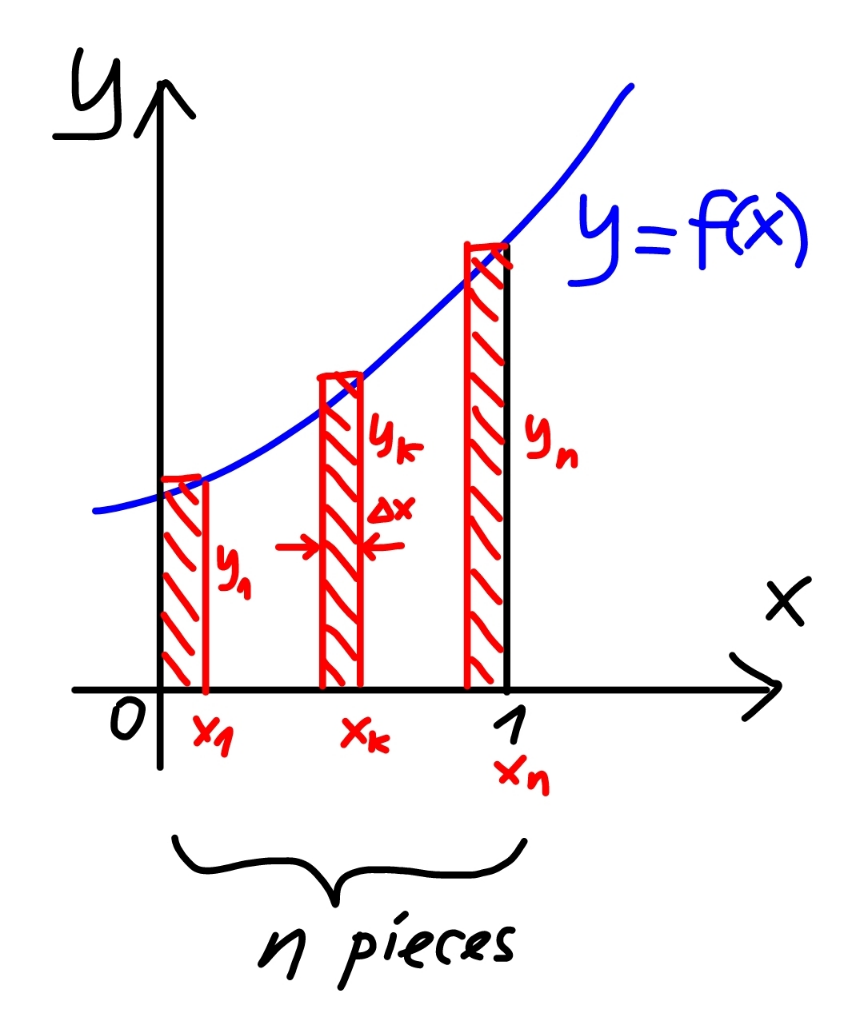
Commented by mr W last updated on 25/Aug/23

generally Δx=(1/n) ∫_0 ^1 f(x)dx≈y_1 Δx+y_2 Δx+...+y_k Δx+...+y_n Δx ∫_0 ^1 f(x)dx≈(y_1 +y_2 +...+y_k +...+y_n )Δx ∫_0 ^1 f(x)dx≈[f(x_1 )+f(x_2 )+...+f(x_k )+...+f(x_n )]Δx ∫_0 ^1 f(x)dx≈[f(Δx)+f(2Δx)+...+f(kΔx)+...+f(nΔx)]Δx ∫_0 ^1 f(x)dx≈[f((1/n))+f((2/b))+...+f((k/n))+...+f((n/n))](1/n) ∫_0 ^1 f(x)dx≈(1/n)Σ_(k=1) ^n f((k/n)) ∫_0 ^1 f(x)dx=lim_(n→∞) [(1/n)Σ_(k=1) ^n f((k/n))] in current case: f(x)=(1/(2+x))

$${generally} \\ $$$$\Delta{x}=\frac{\mathrm{1}}{{n}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\approx{y}_{\mathrm{1}} \Delta{x}+{y}_{\mathrm{2}} \Delta{x}+...+{y}_{{k}} \Delta{x}+...+{y}_{{n}} \Delta{x} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\approx\left({y}_{\mathrm{1}} +{y}_{\mathrm{2}} +...+{y}_{{k}} +...+{y}_{{n}} \right)\Delta{x} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\approx\left[{f}\left({x}_{\mathrm{1}} \right)+{f}\left({x}_{\mathrm{2}} \right)+...+{f}\left({x}_{{k}} \right)+...+{f}\left({x}_{{n}} \right)\right]\Delta{x} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\approx\left[{f}\left(\Delta{x}\right)+{f}\left(\mathrm{2}\Delta{x}\right)+...+{f}\left({k}\Delta{x}\right)+...+{f}\left({n}\Delta{x}\right)\right]\Delta{x} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\approx\left[{f}\left(\frac{\mathrm{1}}{{n}}\right)+{f}\left(\frac{\mathrm{2}}{{b}}\right)+...+{f}\left(\frac{{k}}{{n}}\right)+...+{f}\left(\frac{{n}}{{n}}\right)\right]\frac{\mathrm{1}}{{n}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\approx\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{f}\left(\frac{{k}}{{n}}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{f}\left(\frac{{k}}{{n}}\right)\right] \\ $$$${in}\:{current}\:{case}:\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}+{x}} \\ $$

Commented by Tawa11 last updated on 25/Aug/23

Wow, I really appreciate sir.

$$\mathrm{Wow},\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com