
Question Number 101770 by john santu last updated on 04/Jul/20
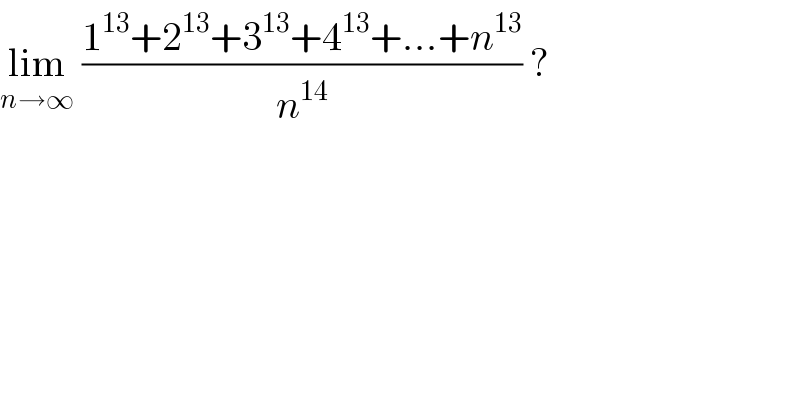
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}^{\mathrm{13}} +\mathrm{2}^{\mathrm{13}} +\mathrm{3}^{\mathrm{13}} +\mathrm{4}^{\mathrm{13}} +...+{n}^{\mathrm{13}} }{{n}^{\mathrm{14}} }\:? \\ $$
Commented by Dwaipayan Shikari last updated on 04/Jul/20

$$\frac{\mathrm{1}}{\mathrm{14}} \\ $$
Commented by john santu last updated on 04/Jul/20

$${yes}.\:{n}\rightarrow\infty.\:{typo}. \\ $$
Answered by bemath last updated on 05/Jul/20
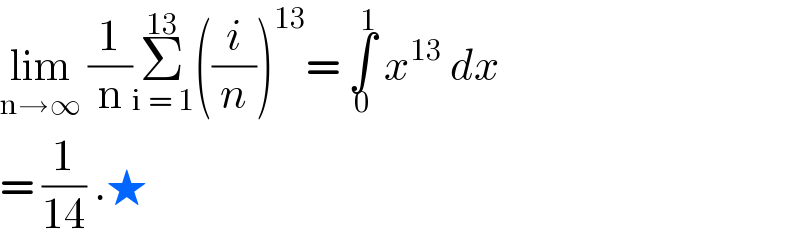
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{i}\:=\:\mathrm{1}} {\overset{\mathrm{13}} {\sum}}\left(\frac{{i}}{{n}}\right)^{\mathrm{13}} =\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:{x}^{\mathrm{13}} \:{dx}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{14}}\:.\bigstar\: \\ $$
