
Question Number 114020 by bemath last updated on 16/Sep/20
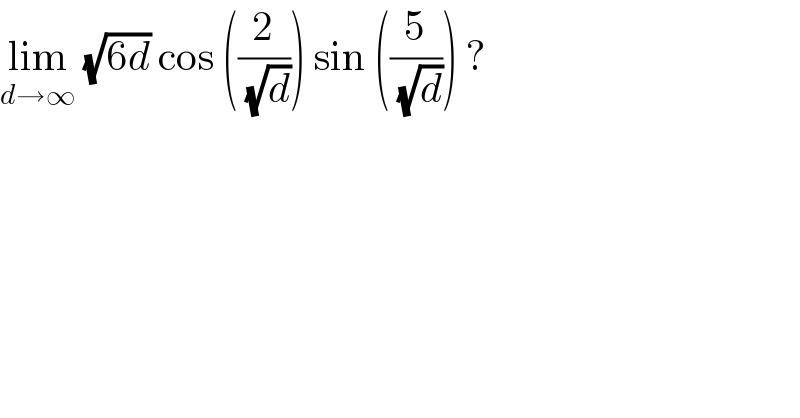
$$\underset{{d}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{6}{d}}\:\mathrm{cos}\:\left(\frac{\mathrm{2}}{\:\sqrt{{d}}}\right)\:\mathrm{sin}\:\left(\frac{\mathrm{5}}{\:\sqrt{{d}}}\right)\:?\: \\ $$$$ \\ $$
Answered by Olaf last updated on 17/Sep/20
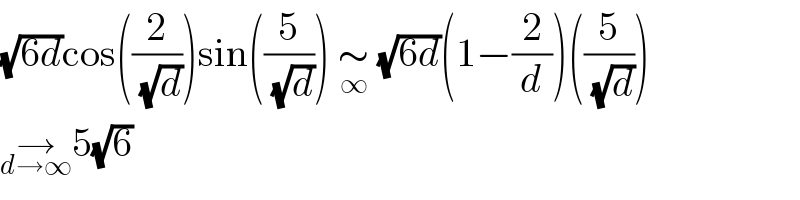
$$\sqrt{\mathrm{6}{d}}\mathrm{cos}\left(\frac{\mathrm{2}}{\:\sqrt{{d}}}\right)\mathrm{sin}\left(\frac{\mathrm{5}}{\:\sqrt{{d}}}\right)\:\underset{\infty} {\sim}\:\sqrt{\mathrm{6}{d}}\left(\mathrm{1}−\frac{\mathrm{2}}{{d}}\right)\left(\frac{\mathrm{5}}{\:\sqrt{{d}}}\right) \\ $$$$\underset{{d}\rightarrow\infty} {\rightarrow}\mathrm{5}\sqrt{\mathrm{6}} \\ $$
Answered by mathmax by abdo last updated on 16/Sep/20
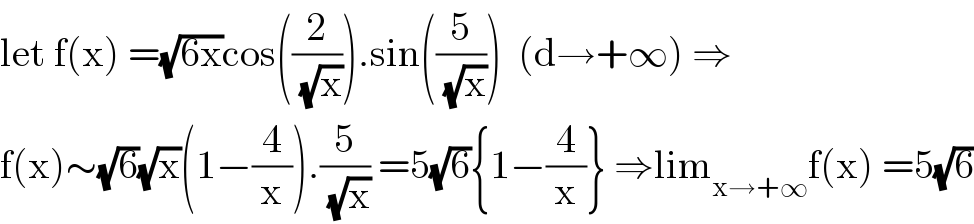
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\sqrt{\mathrm{6x}}\mathrm{cos}\left(\frac{\mathrm{2}}{\sqrt{\mathrm{x}}}\right).\mathrm{sin}\left(\frac{\mathrm{5}}{\sqrt{\mathrm{x}}}\right)\:\:\left(\mathrm{d}\rightarrow+\infty\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\sqrt{\mathrm{6}}\sqrt{\mathrm{x}}\left(\mathrm{1}−\frac{\mathrm{4}}{\mathrm{x}}\right).\frac{\mathrm{5}}{\sqrt{\mathrm{x}}}\:=\mathrm{5}\sqrt{\mathrm{6}}\left\{\mathrm{1}−\frac{\mathrm{4}}{\mathrm{x}}\right\}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{5}\sqrt{\mathrm{6}} \\ $$
Answered by bobhans last updated on 17/Sep/20
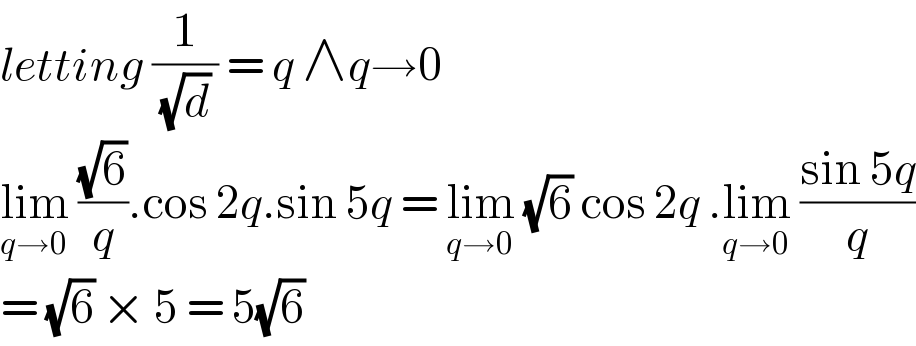
$${letting}\:\frac{\mathrm{1}}{\:\sqrt{{d}}\:}\:=\:{q}\:\wedge{q}\rightarrow\mathrm{0} \\ $$$$\underset{{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{6}}}{{q}}.\mathrm{cos}\:\mathrm{2}{q}.\mathrm{sin}\:\mathrm{5}{q}\:=\:\underset{{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{\mathrm{6}}\:\mathrm{cos}\:\mathrm{2}{q}\:.\underset{{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{5}{q}}{{q}} \\ $$$$=\:\sqrt{\mathrm{6}}\:×\:\mathrm{5}\:=\:\mathrm{5}\sqrt{\mathrm{6}} \\ $$
