
Question Number 212169 by universe last updated on 04/Oct/24
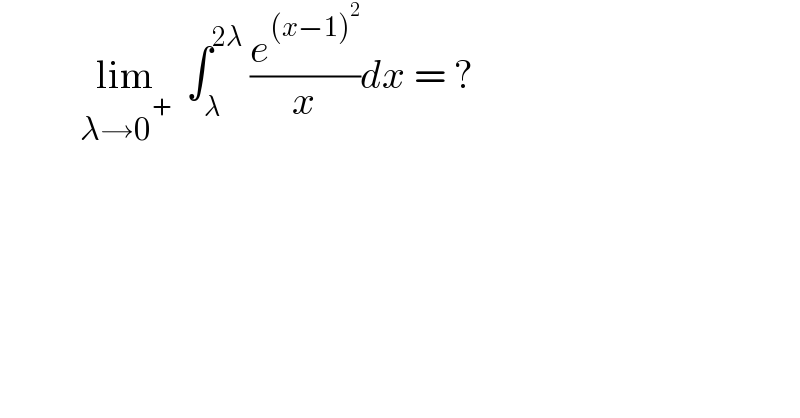
$$\:\:\:\:\:\:\:\:\:\:\underset{\lambda\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\:\int_{\lambda} ^{\mathrm{2}\lambda} \:\frac{{e}^{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } }{{x}}{dx}\:=\:? \\ $$
Answered by MrGaster last updated on 03/Nov/24
![=lim_(λ→0^+ ) ∫_1 ^2 (e^((λu−1)^2 ) /(λu))λdu =lim_(λ→0^+ ) (e^(λ^2 u^2 −2λu+1) /u)du =∫_1 ^2 (e^1 /u)du =e[ln u]_1 ^2 =e(ln 2−ln 1) =e ln 2](Q213363.png)
$$=\underset{\lambda\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{e}^{\left(\lambda{u}−\mathrm{1}\right)^{\mathrm{2}} } }{\lambda{u}}\lambda{du} \\ $$$$=\underset{\lambda\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{e}^{\lambda^{\mathrm{2}} {u}^{\mathrm{2}} \:−\mathrm{2}\lambda{u}+\mathrm{1}} }{{u}}{du} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{e}^{\mathrm{1}} }{{u}}{du} \\ $$$$={e}\left[\mathrm{ln}\:{u}\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$={e}\left(\mathrm{ln}\:\mathrm{2}−\mathrm{ln}\:\mathrm{1}\right) \\ $$$$={e}\:\mathrm{ln}\:\mathrm{2} \\ $$
