Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 49244 by maxmathsup by imad last updated on 04/Dec/18

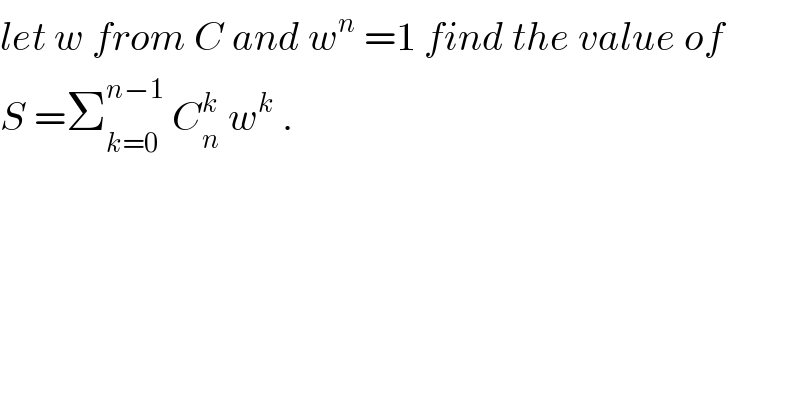
let w from C and w^n =1 find the value of S =Σ_(k=0) ^(n−1) C_n ^k w^k .

$${let}\:{w}\:{from}\:{C}\:{and}\:{w}^{{n}} \:=\mathrm{1}\:{find}\:{the}\:{value}\:{of}\: \\ $$$${S}\:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{C}_{{n}} ^{{k}} \:{w}^{{k}} \:. \\ $$

Answered by Smail last updated on 05/Dec/18

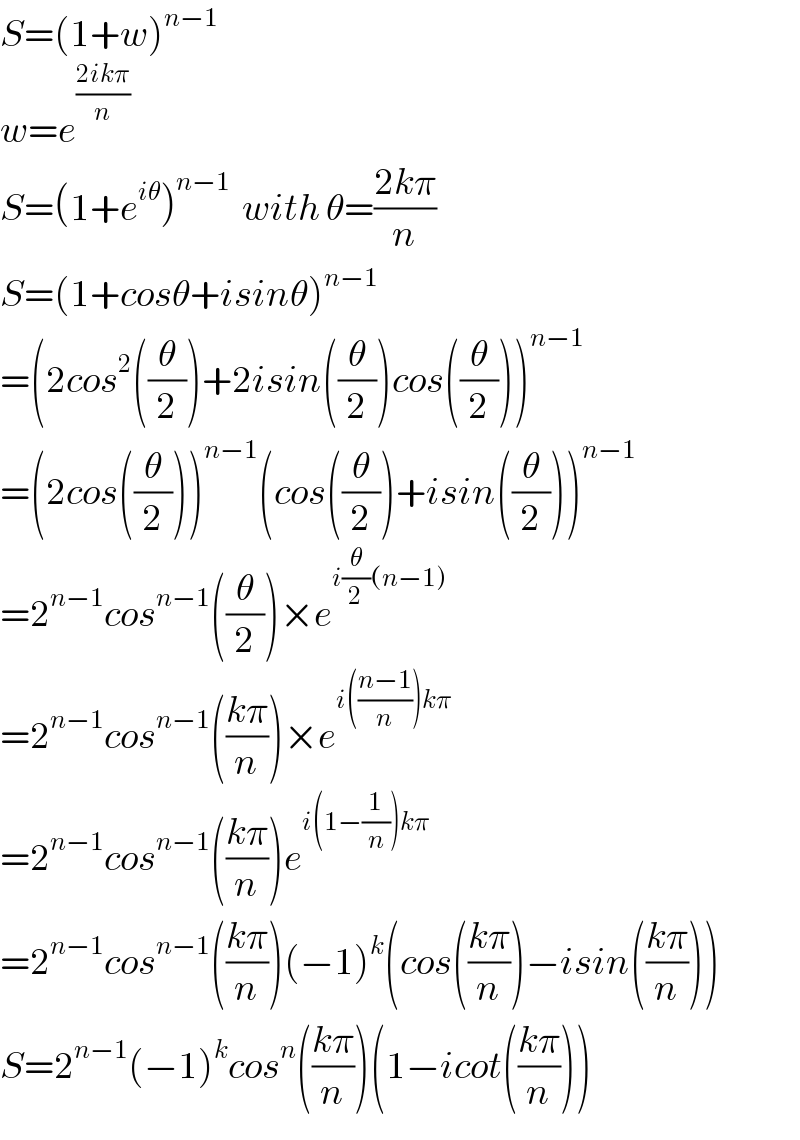
S=(1+w)^(n−1) w=e^((2ikπ)/n) S=(1+e^(iθ) )^(n−1) with θ=((2kπ)/n) S=(1+cosθ+isinθ)^(n−1) =(2cos^2 ((θ/2))+2isin((θ/2))cos((θ/2)))^(n−1) =(2cos((θ/2)))^(n−1) (cos((θ/2))+isin((θ/2)))^(n−1) =2^(n−1) cos^(n−1) ((θ/2))×e^(i(θ/2)(n−1)) =2^(n−1) cos^(n−1) (((kπ)/n))×e^(i(((n−1)/n))kπ) =2^(n−1) cos^(n−1) (((kπ)/n))e^(i(1−(1/n))kπ) =2^(n−1) cos^(n−1) (((kπ)/n))(−1)^k (cos(((kπ)/n))−isin(((kπ)/n))) S=2^(n−1) (−1)^k cos^n (((kπ)/n))(1−icot(((kπ)/n)))

$${S}=\left(\mathrm{1}+{w}\right)^{{n}−\mathrm{1}} \\ $$$${w}={e}^{\frac{\mathrm{2}{ik}\pi}{{n}}} \\ $$$${S}=\left(\mathrm{1}+{e}^{{i}\theta} \right)^{{n}−\mathrm{1}} \:\:{with}\:\theta=\frac{\mathrm{2}{k}\pi}{{n}} \\ $$$${S}=\left(\mathrm{1}+{cos}\theta+{isin}\theta\right)^{{n}−\mathrm{1}} \\ $$$$=\left(\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)+\mathrm{2}{isin}\left(\frac{\theta}{\mathrm{2}}\right){cos}\left(\frac{\theta}{\mathrm{2}}\right)\right)^{{n}−\mathrm{1}} \\ $$$$=\left(\mathrm{2}{cos}\left(\frac{\theta}{\mathrm{2}}\right)\right)^{{n}−\mathrm{1}} \left({cos}\left(\frac{\theta}{\mathrm{2}}\right)+{isin}\left(\frac{\theta}{\mathrm{2}}\right)\right)^{{n}−\mathrm{1}} \\ $$$$=\mathrm{2}^{{n}−\mathrm{1}} {cos}^{{n}−\mathrm{1}} \left(\frac{\theta}{\mathrm{2}}\right)×{e}^{{i}\frac{\theta}{\mathrm{2}}\left({n}−\mathrm{1}\right)} \\ $$$$=\mathrm{2}^{{n}−\mathrm{1}} {cos}^{{n}−\mathrm{1}} \left(\frac{{k}\pi}{{n}}\right)×{e}^{{i}\left(\frac{{n}−\mathrm{1}}{{n}}\right){k}\pi} \\ $$$$=\mathrm{2}^{{n}−\mathrm{1}} {cos}^{{n}−\mathrm{1}} \left(\frac{{k}\pi}{{n}}\right){e}^{{i}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right){k}\pi} \\ $$$$=\mathrm{2}^{{n}−\mathrm{1}} {cos}^{{n}−\mathrm{1}} \left(\frac{{k}\pi}{{n}}\right)\left(−\mathrm{1}\right)^{{k}} \left({cos}\left(\frac{{k}\pi}{{n}}\right)−{isin}\left(\frac{{k}\pi}{{n}}\right)\right) \\ $$$${S}=\mathrm{2}^{{n}−\mathrm{1}} \left(−\mathrm{1}\right)^{{k}} {cos}^{{n}} \left(\frac{{k}\pi}{{n}}\right)\left(\mathrm{1}−{icot}\left(\frac{{k}\pi}{{n}}\right)\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com