
Previous in Relation and Functions Next in Relation and Functions
Question Number 52675 by maxmathsup by imad last updated on 11/Jan/19
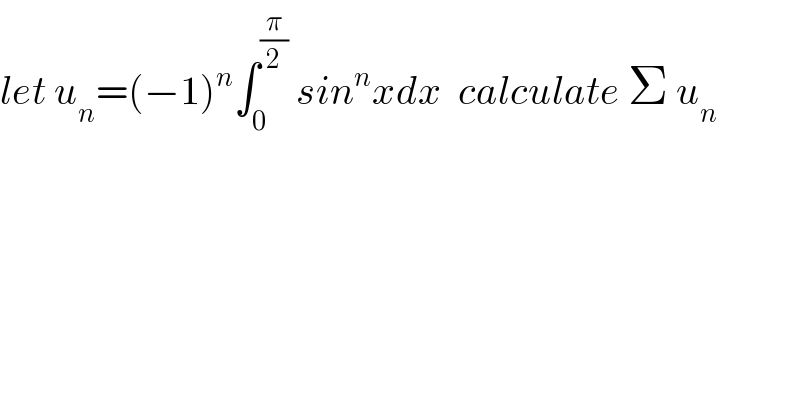
$${let}\:{u}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}^{{n}} {xdx}\:\:{calculate}\:\Sigma\:{u}_{{n}} \\ $$
Commented by maxmathsup by imad last updated on 11/Jan/19
![we have Σ_(n=0) ^∞ u_n =Σ_(n=0) ^∞ ∫_0 ^(π/2) (−sinx)^n dx =∫_0 ^(π/2) (Σ_(n=0) ^∞ (−sinx)^n )dx =∫_0 ^(π/2) (dx/(1+sinx)) =_(tan((x/(2 )))=t) ∫_0 ^1 (1/(1+((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) =2 ∫_0 ^1 (dt/(1+t^2 +2t)) =2 ∫_0 ^1 (dt/((t+1)^2 )) =2[−(1/(t+1))]_0 ^1 =2(1−(1/2)) = 1 ⇒ Σ_(n=0) ^∞ u_n =1 .](Q52707.png)
$${we}\:{have}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}_{{n}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(−{sinx}\right)^{{n}} {dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\sum_{{n}=\mathrm{0}} ^{\infty} \left(−{sinx}\right)^{{n}} \right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dx}}{\mathrm{1}+{sinx}}\:\:=_{{tan}\left(\frac{{x}}{\mathrm{2}\:}\right)={t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} \:+\mathrm{2}{t}} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{2}\left[−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\mathrm{1}\:\Rightarrow\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}_{{n}} =\mathrm{1}\:. \\ $$
